| << Chapter < Page | Chapter >> Page > |
Suppose is a random variable with a distribution that may be known or unknown (it can be any distribution) and suppose:
~
The Central Limit Theorem for Sums says that if you keep drawing larger and larger samples and taking their sums, the sums form their own normal distribution (the sampling distribution) which approaches a normal distribution as the sample size increases. The normal distribution has a mean equal to the original mean multiplied by the sample size and a standard deviationequal to the original standard deviation multiplied by the square root of the sample size.
The random variable has the following z-score associated with it:
An unknown distribution has a mean of 90 and a standard deviation of 15. A sample of size 80 is drawn randomly from the population.
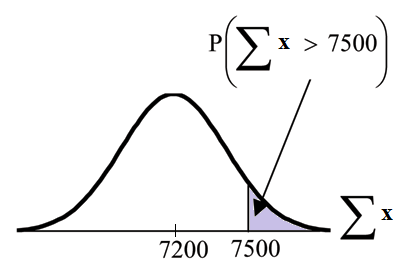
Let = one value from the original unknown population. The probability question asks you to find a probability for the sum (or total of) 80 values.
= the sum or total of 80 values. Since , , and , then
~
normalcdf (lower value, upper value, mean of sums,
stdev of sums)
The parameter list is abbreviated (lower, upper, )
normalcdf (7500,1E99,
Reminder:
. Press the
EE key for E.

Notification Switch
Would you like to follow the 'Collaborative statistics (custom lecture version modified by t. short)' conversation and receive update notifications?