| << Chapter < Page | Chapter >> Page > |
To find the direction of the induced field, the direction of the current, and the polarity of the induced emf, we apply Lenz’s law as explained in Faraday's Law of Induction: Lenz's Law . (See [link] (b).) Flux is increasing, since the area enclosed is increasing. Thus the induced field must oppose the existing one and be out of the page. And so the RHR-2 requires that I be counterclockwise, which in turn means the top of the rod is positive as shown.
Motional emf also occurs if the magnetic field moves and the rod (or other object) is stationary relative to the Earth (or some observer). We have seen an example of this in the situation where a moving magnet induces an emf in a stationary coil. It is the relative motion that is important. What is emerging in these observations is a connection between magnetic and electric fields. A moving magnetic field produces an electric field through its induced emf. We already have seen that a moving electric field produces a magnetic field—moving charge implies moving electric field and moving charge produces a magnetic field.
Motional emfs in the Earth’s weak magnetic field are not ordinarily very large, or we would notice voltage along metal rods, such as a screwdriver, during ordinary motions. For example, a simple calculation of the motional emf of a 1 m rod moving at 3.0 m/s perpendicular to the Earth’s field gives . This small value is consistent with experience. There is a spectacular exception, however. In 1992 and 1996, attempts were made with the space shuttle to create large motional emfs. The Tethered Satellite was to be let out on a 20 km length of wire as shown in [link] , to create a 5 kV emf by moving at orbital speed through the Earth’s field. This emf could be used to convert some of the shuttle’s kinetic and potential energy into electrical energy if a complete circuit could be made. To complete the circuit, the stationary ionosphere was to supply a return path for the current to flow. (The ionosphere is the rarefied and partially ionized atmosphere at orbital altitudes. It conducts because of the ionization. The ionosphere serves the same function as the stationary rails and connecting resistor in [link] , without which there would not be a complete circuit.) Drag on the current in the cable due to the magnetic force does the work that reduces the shuttle’s kinetic and potential energy and allows it to be converted to electrical energy. The tests were both unsuccessful. In the first, the cable hung up and could only be extended a couple of hundred meters; in the second, the cable broke when almost fully extended. [link] indicates feasibility in principle.
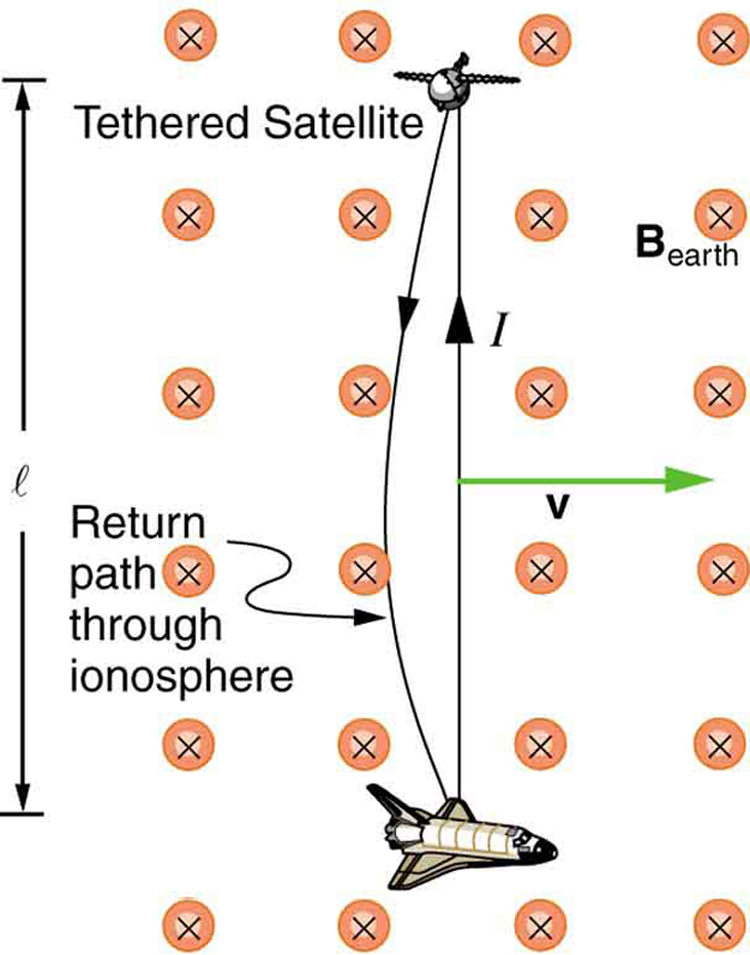
Calculate the motional emf induced along a 20.0 km long conductor moving at an orbital speed of 7.80 km/s perpendicular to the Earth’s magnetic field.
Strategy
This is a straightforward application of the expression for motional emf— .
Solution
Entering the given values into gives
Discussion
The value obtained is greater than the 5 kV measured voltage for the shuttle experiment, since the actual orbital motion of the tether is not perpendicular to the Earth’s field. The 7.80 kV value is the maximum emf obtained when and .

Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?