| << Chapter < Page | Chapter >> Page > |
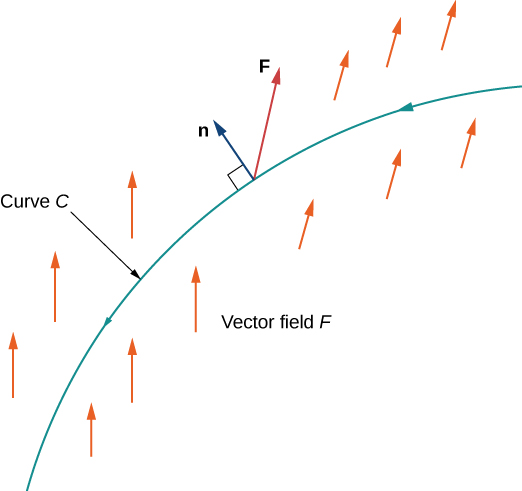
We now give a formula for calculating the flux across a curve. This formula is analogous to the formula used to calculate a vector line integral (see [link] ).
Let F be a vector field and let C be a smooth curve with parameterization Let The flux of F across C is
The proof of [link] is similar to the proof of [link] . Before deriving the formula, note that Therefore,
□
Calculate the flux of across a unit circle oriented counterclockwise ( [link] ).

To compute the flux, we first need a parameterization of the unit circle. We can use the standard parameterization The normal vector to a unit circle is Therefore, the flux is
Calculate the flux of across the line segment from to where the curve is oriented from left to right.
3/2
Let be a two-dimensional vector field. Recall that integral is sometimes written as Analogously, flux is sometimes written in the notation because the unit normal vector N is perpendicular to the unit tangent T . Rotating the vector by 90° results in vector Therefore, the line integral in [link] can be written as
Now that we have defined flux, we can turn our attention to circulation. The line integral of vector field F along an oriented closed curve is called the circulation of F along C . Circulation line integrals have their own notation: The circle on the integral symbol denotes that C is “circular” in that it has no endpoints. [link] shows a calculation of circulation.
To see where the term circulation comes from and what it measures, let v represent the velocity field of a fluid and let C be an oriented closed curve. At a particular point P , the closer the direction of v ( P ) is to the direction of T ( P ), the larger the value of the dot product The maximum value of occurs when the two vectors are pointing in the exact same direction; the minimum value of occurs when the two vectors are pointing in opposite directions. Thus, the value of the circulation measures the tendency of the fluid to move in the direction of C .
Let be the vector field from [link] and let C represent the unit circle oriented counterclockwise. Calculate the circulation of F along C .
We use the standard parameterization of the unit circle: Then, and Therefore, the circulation of F along C is
Notice that the circulation is positive. The reason for this is that the orientation of C “flows” with the direction of F . At any point along the circle, the tangent vector and the vector from F form an angle of less than 90°, and therefore the corresponding dot product is positive.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?