| << Chapter < Page | Chapter >> Page > |
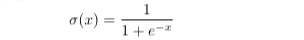
The sigmoid activation function is the most general nonlinear activation function used in neural networks. Intuition would naively suggest that the activation of a neuron would be well modeled by the step function, but the issue is its non-differentiability. The stochastic gradient descent algorithm requires that activation functions be differentiable. The solution would be to approximate the step function using a smooth function like the sigmoid or the hyperbolic tangent. The issue with the sigmoid function is that its derivative far from the origin is near zero, so if any individual weight on a neuron is very wrong, it is unable to use the gradient to adjust its value. As a result, outlier weights can significantly impact the performance of the network.
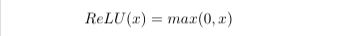
The advantage of using rectified linear units is threefold. First, its derivative is a constant (either 0 or 1) making the computation of the gradient much faster. Second, it is a better approximation of how biological neurons fire, in the sense that there is no activation in the absence of stimulation. Third, rectified linear units speed up learning by not being able to fire with zero net excitation. This means that if an excitation fails to overcome a neuron’s bias, the neuron will not fire at all. And when it does fire, the activation is linearly proportional to the excitation. The sigmoid function in comparison allows for some activation to occur with zero and even negative net excitation. However, a lower learning rate needs to be used with ReLU because its zero derivative for a net excitation less than zero means that the neuron effectively stops learning once its net excitation hits zero.
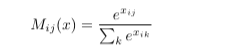
Softmax activation is particularly useful on the output layer, as it normalizes the output. Exponentiating each of the net excitations gives a more dramatic representation of the differences between them. Weak excitations become weaker activations and strong excitations become stronger activations. Everything is then normalized, giving the layer the effect of becoming a decision-maker.
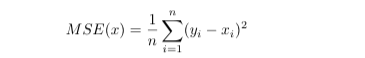
Mean-squared error is the simplest measurement of difference that can be used to good effect in a neural network. It can be used with any activation function and is the more versatile option, though not always the most effective one. One of its shortcomings is that neurons with a sigmoid activation function become saturated quickly and are unable to learn more as a result of the relatively small magnitude of the sigmoid’s derivative far from the origin.
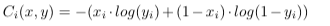
Cross-entropy treats the desired output as some probability distribution and the network’s output as another probability distribution, and measures the distance between the distributions. The main attraction to using cross-entropy is that when used in conjunction with the sigmoid activation function, its gradient is linearly dependent on the error, solving the issue with neurons becoming saturated quickly.
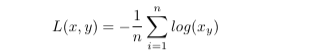
Log likelihood maximizes only the output neuron corresponding to which neuron should be firing. Used in conjunction with a softmax layer, all other output neurons would be minimized as a result of maximizing the desired output neuron. In this sense, a softmax layer has to be used, or the activations of the final layer will be too close together to draw meaningful conclusions.
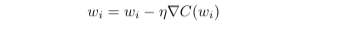
Stochastic gradient descent is the algorithm used in our network to adjust weights and biases according to the evaluation of the gradient of a given cost function. The gradient determines whether a parameter should increase or decrease and by how much. The learning rate of a network is a constant associated with how much a parameter should travel down its gradient at each reevaluation. In the original algorithm, parameters are updated after each given input. A common practice with neural nets is to only reevaluate the gradient after a so-called minibatch of multiple inputs is passed. This way, the cost function has multiple samples and can better construct a curve, yet the gradient is somewhat different every time it’s evaluated. This introduces some noise into the gradient to make it harder for parameters to get stuck in a local minimum of the gradient.

Notification Switch
Would you like to follow the 'Elec 301 projects fall 2015' conversation and receive update notifications?