| << Chapter < Page | Chapter >> Page > |
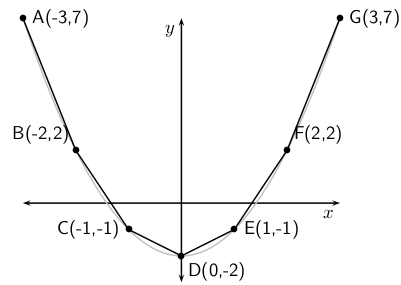
Fill in the table by calculating the average gradient over the indicated intervals for the function :
| A-B | |||||
| B-C | |||||
| C-D | |||||
| D-E | |||||
| E-F | |||||
| F-G |
What do you notice about the average gradient over each interval? What can you say about the average gradients between A and D compared to the averagegradients between D and G?

The average gradient of a parabolic function depends on the interval and is the gradient of a straight line that passes through the points on the interval.
For example, in [link] the various points have been joined by straight-lines. The average gradients between the joined points are then the gradients of the straight lines that pass through the points.
Given the equation of a curve and two points ( , ):
Find the average gradient of the curve between the points and
Label the points as follows:
to make it easier to calculate the gradient.
We use the equation for the curve to calculate the -value at and .
The average gradient between and on the curve is 0.
We can extend the concept of average gradient to any function. The average gradient for any function also depends on the interval chosen and is the gradient of a straight line that passes through the two points. So we can use the formula that we found for the average gradient of parabolic functions and apply it to any function. We will consider the average gradient of just two functions here: exponential functions and hyperbolic functions.
For example, if we were asked to find the average gradient of the function
between the points
and
. This is shown in
[link] .

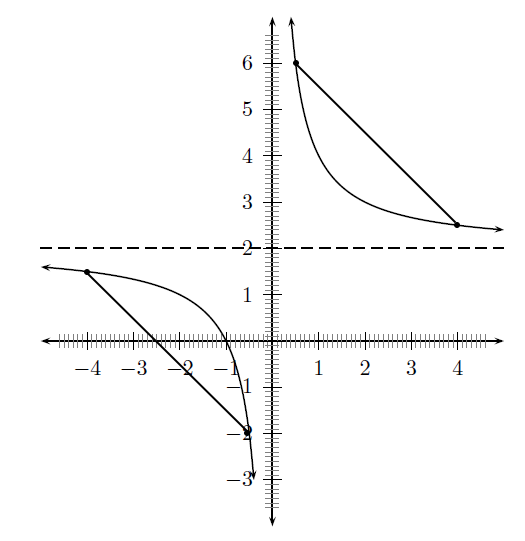
For example, if we were asked to find the average gradient of the function
between the points
and
and
and
. This is shown in
[link] .
For the first point we would get:

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?