5.7 Change of variables in multiple integrals (Page 2/13)

Calculus volume 3 Page 2 / 13

Finding the image under $T$

Let the transformation $T$ be defined by $T (u, v) = (x, y)$ where $x = u^{2} - v^{2}$ and $y = u v .$ Find the image of the triangle in the $u v -plane$ with vertices $(0, 0), (0, 1),$ and $(1, 1) .$

The triangle and its image are shown in [link] . To understand how the sides of the triangle transform, call the side that joins $(0, 0)$ and $(0, 1)$ side $A,$ the side that joins $(0, 0)$ and $(1, 1)$ side $B,$ and the side that joins $(1, 1)$ and $(0, 1)$ side $C .$

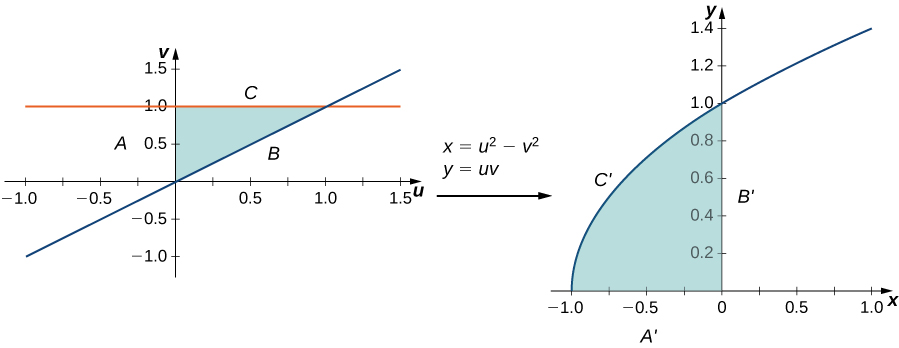
On the left-hand side of this figure, there is a triangular region given in the Cartesian uv-plane with boundaries A, B, and C represented by the v axis, the line u = v, and the line v = 1, respectively. Then there is an arrow from this graph to the right-hand side of the figure marked with x = u squared minus v squared and y = u v. On the right-hand side of this figure there is a complex region given in the Cartesian x y-plane with boundaries A’, B’, and C’ given by the x axis, y axis, and a line curving from (negative 1, 0) through (0, 1), namely x = y squared minus 1, respectively. — A triangular region in the $u v -plane$ is transformed into an image in the $x y -plane .$

For the side $A : u = 0, 0 \leq v \leq 1$ transforms to $x = − v^{2}, y = 0$ so this is the side $A'$ that joins $(−1, 0)$ and $(0, 0) .$

For the side $B : u = v, 0 \leq u \leq 1$ transforms to $x = 0, y = u^{2}$ so this is the side $B^{'}$ that joins $(0, 0)$ and $(0, 1) .$

For the side $C : 0 \leq u \leq 1, v = 1$ transforms to $x = u^{2} - 1, y = u$ (hence $x = y^{2} - 1)$ so this is the side $C^{'}$ that makes the upper half of the parabolic arc joining $(−1, 0)$ and $(0, 1) .$

All the points in the entire region of the triangle in the $u v -plane$ are mapped inside the parabolic region in the $x y -plane .$

Got questions? Get instant answers now!

Let a transformation $T$ be defined as $T (u, v) = (x, y)$ where $x = u + v, y = 3 v .$ Find the image of the rectangle $G = {(u, v) : 0 \leq u \leq 1, 0 \leq v \leq 2}$ from the $u v -plane$ after the transformation into a region $R$ in the $x y -plane .$ Show that $T$ is a one-to-one transformation and find $T^{−1} (x, y) .$

$T^{−1} (x, y) = (u, v)$ where $u = \frac{3 x - y}{3}$ and $v = \frac{y}{3}$

Got questions? Get instant answers now!

Jacobians

Recall that we mentioned near the beginning of this section that each of the component functions must have continuous first partial derivatives, which means that $g_{u}, g_{v}, h_{u},$ and $h_{v}$ exist and are also continuous. A transformation that has this property is called a $C^{1}$ transformation (here $C$ denotes continuous). Let $T (u, v) = (g (u, v), h (u, v)),$ where $x = g (u, v)$ and $y = h (u, v),$ be a one-to-one $C^{1}$ transformation. We want to see how it transforms a small rectangular region $S,$ $Δ u$ units by $Δ v$ units, in the $u v -plane$ (see the following figure).

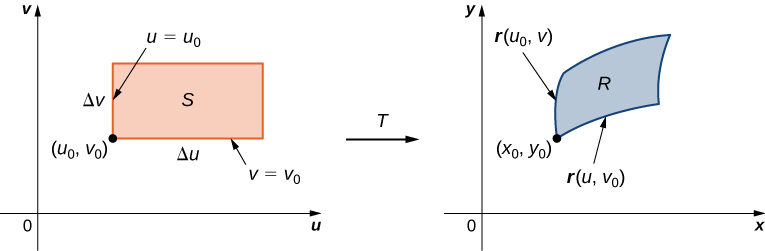
On the left-hand side of this figure, there is a region S with lower right corner point (u sub 0, v sub 0), height Delta v, and length Delta u given in the Cartesian u v-plane. Then there is an arrow from this graph to the right-hand side of the figure marked with T. On the right-hand side of this figure there is a region R with point (x sub 0, y sub 0) given in the Cartesian x y-plane with sides r(u, v sub 0) along the bottom and r(u sub 0, v) along the left. — A small rectangle $S$ in the $u v -plane$ is transformed into a region $R$ in the $x y -plane .$

Since $x = g (u, v)$ and $y = h (u, v),$ we have the position vector $r (u, v) = g (u, v) i + h (u, v) j$ of the image of the point $(u, v) .$ Suppose that $(u_{0}, v_{0})$ is the coordinate of the point at the lower left corner that mapped to $(x_{0}, y_{0}) = T (u_{0}, v_{0}) .$ The line $v = v_{0}$ maps to the image curve with vector function $r (u, v_{0}),$ and the tangent vector at $(x_{0}, y_{0})$ to the image curve is

r_{u} = g_{u} (u_{0}, v_{0}) i + h_{u} (u_{0}, v_{0}) j = \frac{\partial x}{\partial u} i + \frac{\partial y}{\partial u} j .

Similarly, the line $u = u_{0}$ maps to the image curve with vector function $r (u_{0}, v),$ and the tangent vector at $(x_{0}, y_{0})$ to the image curve is

r_{v} = g_{v} (u_{0}, v_{0}) i + h_{v} (u_{0}, v_{0}) j = \frac{\partial x}{\partial v} i + \frac{\partial y}{\partial v} j .

Now, note that

r_{u} = lim_{Δ u \to 0} \frac{r (u_{0} + Δ u, v_{0}) - r (u_{0}, v_{0})}{Δ u} so r (u_{0} + Δ u, v_{0}) - r (u_{0}, v_{0}) \approx Δ u r_{u} .

Similarly,

r_{v} = lim_{Δ v \to 0} \frac{r (u_{0}, v_{0} + Δ v) - r (u_{0}, v_{0})}{Δ v} so r (u_{0}, v_{0} + Δ v) - r (u_{0}, v_{0}) \approx Δ v r_{v} .

This allows us to estimate the area $Δ A$ of the image $R$ by finding the area of the parallelogram formed by the sides $Δ v r_{v}$ and $Δ u r_{u} .$ By using the cross product of these two vectors by adding the k th component as $0,$ the area $Δ A$ of the image $R$ (refer to The Cross Product ) is approximately $| Δ u r_{u} \times Δ v r_{v} | = | r_{u} \times r_{v} | Δ u Δ v .$ In determinant form, the cross product is

r_{u} \times r_{v} = | \begin{matrix} i & j & k \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0 \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \end{matrix} | = | \begin{array}{l} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{array} | k = (\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}) k .

Since $| k | = 1,$ we have $Δ A \approx | r_{u} \times r_{v} | Δ u Δ v = (\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}) Δ u Δ v .$

Definition

The Jacobian of the $C^{1}$ transformation $T (u, v) = (g (u, v), h (u, v))$ is denoted by $J (u, v)$ and is defined by the $2 \times 2$ determinant

J (u, v) = | \frac{\partial (x, y)}{\partial (u, v)} | = | \begin{array}{l} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{array} | = (\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}) .

<< Chapter < Page Page > Chapter >>

Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	Summer kitchens By Heather McAvoy Start Quiz
	8 Arts Society: Theater 8 By Jonathan Long Start Quiz
	6 BOD Respiratory Exam By Brooke Delaney Start Exam
	Principles of microeconomics for ap® courses By OpenStax Read Online Course
©flickr: Hey	Anatomy Physiology Final By Joli Julianna Start Test
	20 Sociology 20 Population Urbanization Environment By OpenStax Start Quiz
	Social Dances 1 By Marion Cabalfin Start Test
	11 Biology 11 Meiosis Sexual Reproduction MCQ By OpenStax Start Quiz
	23 Pesticides/Small animal poison Test By Brooke Delaney Start Exam
	Introduction to sociology 2e By OpenStax Read Online Course