5.6 Calculating centers of mass and moments of inertia  (Page 2/8)

Now that we have established the expression for mass, we have the tools we need for calculating moments and centers of mass. The moment $M_x$ about the $x\text{-axis}$ for $R$ is the limit of the sums of moments of the regions $R_{ij}$ about the $x\text{-axis}\text{.}$ Hence

Similarly, the moment $M_y$ about the $y\text{-axis}$ for $R$ is the limit of the sums of moments of the regions $R_{ij}$ about the $y\text{-axis}\text{.}$ Hence

Finally we are ready to restate the expressions for the center of mass in terms of integrals. We denote the x -coordinate of the center of mass by $\stackrel{\text{−}}{x}$ and the y -coordinate by $\stackrel{\text{−}}{y}.$ Specifically,

Once again, based on the comments at the end of [link] , we have expressions for the centroid of a region on the plane:

We should use these formulas and verify the centroid of the triangular region $R$ referred to in the last three examples.

Finding mass, moments, and center of mass

Find the mass, moments, and the center of mass of the lamina of density $\rho \left(x,y\right)=x+y$ occupying the region $R$ under the curve $y=x^2$ in the interval $0\le x\le 2$ (see the following figure).

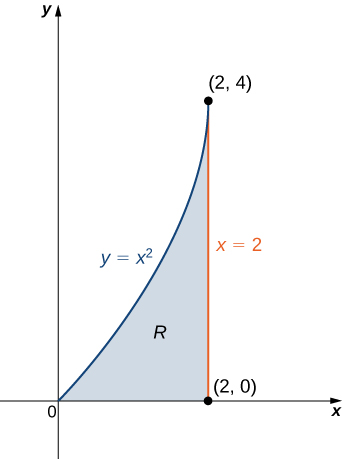
First we compute the mass $m.$ We need to describe the region between the graph of $y=x^2$ and the vertical lines $x=0$ and $x=2\text{:}$

$\begin{array}{cc}\hfill m& ={\displaystyle \underset{R}{\iint }dm}={\displaystyle \underset{R}{\iint }\rho \left(x,y\right)dA={\displaystyle \underset{x=0}{\overset{x=2}{\int }}{\displaystyle \underset{y=0}{\overset{y=x^2}{\int }}\left(x+y\right)dydx={\displaystyle \underset{x=0}{\overset{x=2}{\int }}\left[{xy+\frac{y^2}{2}|}_{y=0}^{y=x^2}\right]}}}}dx\hfill \\ & ={\displaystyle \underset{x=0}{\overset{x=2}{\int }}\left[x^3+\frac{x^4}{2}\right]}dx={\left[\frac{x^4}{4}+\frac{x^5}{10}\right]|}_{x=0}^{x=2}=\frac{36}{5}.\hfill \end{array}$

Now compute the moments $M_x$ and $M_y\text{:}$

$M_x={\displaystyle \underset{R}{\iint }y\rho \left(x,y\right)}dA={\displaystyle \underset{x=0}{\overset{x=2}{\int }}{\displaystyle \underset{y=0}{\overset{y=x^2}{\int }}y\left(x+y\right)dydx=\frac{80}{7}}},$

$M_y={\displaystyle \underset{R}{\iint }x\rho \left(x,y\right)}dA={\displaystyle \underset{x=0}{\overset{x=2}{\int }}{\displaystyle \underset{y=0}{\overset{y=x^2}{\int }}x\left(x+y\right)dydx=\frac{176}{15}}}.$

Finally, evaluate the center of mass,

$\begin{array}{}\\ \\ \\ \stackrel{\text{−}}{x}=\frac{M_y}{m}=\frac{{\displaystyle \underset{R}{\iint }x\rho \left(x,y\right)dA}}{{\displaystyle \underset{R}{\iint }\rho \left(x,y\right)dA}}=\frac{176\text{/}15}{36\text{/}5}=\frac{44}{27},\hfill \\ \stackrel{\text{−}}{y}=\frac{M_x}{m}=\frac{{\displaystyle \underset{R}{\iint }y\rho \left(x,y\right)dA}}{{\displaystyle \underset{R}{\iint }\rho \left(x,y\right)dA}}=\frac{80\text{/}7}{36\text{/}5}=\frac{100}{63}.\hfill \end{array}$

Hence the center of mass is $(\stackrel{\text{−}}{x},\stackrel{\text{−}}{y})=\left(\frac{44}{27},\frac{100}{63}\right).$

Got questions? Get instant answers now!

Got questions? Get instant answers now!