5.5 Triple integrals in cylindrical and spherical coordinates (Page 2/12)

Calculus volume 3 Page 2 / 12

Integration in cylindrical coordinates

Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in [link] . These equations will become handy as we proceed with solving problems using triple integrals.

Equations of some common shapes
	Circular cylinder	Circular cone	Sphere	Paraboloid
Rectangular	$x^{2} + y^{2} = c^{2}$	$z^{2} = c^{2} (x^{2} + y^{2})$	$x^{2} + y^{2} + z^{2} = c^{2}$	$z = c (x^{2} + y^{2})$
Cylindrical	$r = c$	$z = c r$	$r^{2} + z^{2} = c^{2}$	$z = c r^{2}$

As before, we start with the simplest bounded region $B$ in $ℝ^{3},$ to describe in cylindrical coordinates, in the form of a cylindrical box, $B = {(r, θ, z) | a \leq r \leq b, α \leq θ \leq β, c \leq z \leq d}$ ( [link] ). Suppose we divide each interval into $l, m and n$ subdivisions such that $Δ r = \frac{b - a}{l}, Δ θ = \frac{β - α}{m},$ and $Δ z = \frac{d - c}{n} .$ Then we can state the following definition for a triple integral in cylindrical coordinates.

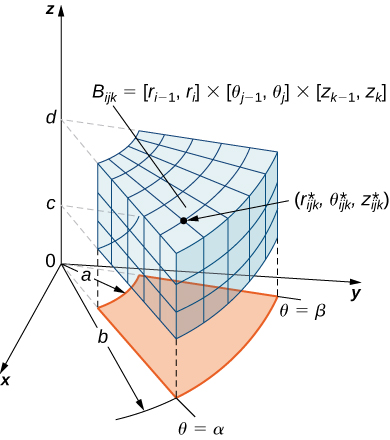
In cylindrical box is shown with its projection onto the polar coordinate plane with inner radius a, outer radius b, and sides defined by theta = alpha and beta. The cylindrical box B starts at height c and goes to height d with the rest of the values the same as the projection onto the plane. — A cylindrical box $B$ described by cylindrical coordinates.

Definition

Consider the cylindrical box (expressed in cylindrical coordinates)

B = {(r, θ, z) | a \leq r \leq b, α \leq θ \leq β, c \leq z \leq d} .

If the function $f (r, θ, z)$ is continuous on $B$ and if $(r_{i j k}^{*}, θ_{i j k}^{*}, z_{i j k}^{*})$ is any sample point in the cylindrical subbox $B_{i j k} = [r_{i - 1}, r_{i}] \times [θ_{j - 1}, θ_{j}] \times [z_{k - 1}, z_{k}]$ ( [link] ), then we can define the triple integral in cylindrical coordinates as the limit of a triple Riemann sum, provided the following limit exists:

lim_{l, m, n \to \infty} \sum_{i = 1}^{l} \sum_{j = 1}^{m} \sum_{k = 1}^{n} f (r_{i j k}^{*}, θ_{i j k}^{*}, z_{i j k}^{*}) r_{i j k}^{*} Δ r Δ θ Δ z .

Note that if $g (x, y, z)$ is the function in rectangular coordinates and the box $B$ is expressed in rectangular coordinates, then the triple integral $\underset{B}{∭} g (x, y, z) d V$ is equal to the triple integral $\underset{B}{∭} g (r cos θ, r sin θ, z) r d r d θ d z$ and we have

\underset{B}{∭} g (x, y, z) d V = \underset{B}{∭} g (r cos θ, r sin θ, z) r d r d θ d z = \underset{B}{∭} f (r, θ, z) r d r d θ d z .

As mentioned in the preceding section, all the properties of a double integral work well in triple integrals, whether in rectangular coordinates or cylindrical coordinates. They also hold for iterated integrals. To reiterate, in cylindrical coordinates, Fubini’s theorem takes the following form:

Fubini’s theorem in cylindrical coordinates

Suppose that $g (x, y, z)$ is continuous on a rectangular box $B,$ which when described in cylindrical coordinates looks like $B = {(r, θ, z) | a \leq r \leq b, α \leq θ \leq β, c \leq z \leq d} .$

Then $g (x, y, z) = g (r cos θ, r sin θ, z) = f (r, θ, z)$ and

\underset{B}{∭} g (x, y, z) d V = \int_{c}^{d} \int_{α}^{β} \int_{a}^{b} f (r, θ, z) r d r d θ d z .

The iterated integral may be replaced equivalently by any one of the other five iterated integrals obtained by integrating with respect to the three variables in other orders.

Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones. Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions.

Evaluating a triple integral over a cylindrical box

Evaluate the triple integral $\underset{B}{∭} (z r sin θ) r d r d θ d z$ where the cylindrical box $B$ is $B = {(r, θ, z) | 0 \leq r \leq 2, 0 \leq θ \leq π / 2, 0 \leq z \leq 4} .$

As stated in Fubini’s theorem, we can write the triple integral as the iterated integral

\underset{B}{∭} (z r sin θ) r d r d θ d z = \int_{θ = 0}^{θ = π / 2} \int_{r = 0}^{r = 2} \int_{z = 0}^{z = 4} (z r sin θ) r d z d r d θ .

The evaluation of the iterated integral is straightforward. Each variable in the integral is independent of the others, so we can integrate each variable separately and multiply the results together. This makes the computation much easier:

\begin{matrix} \int_{θ = 0}^{θ = π / 2} \int_{r = 0}^{r = 2} \int_{z = 0}^{z = 4} (z r sin θ) r d z d r d θ \\ = (\int_{0}^{π / 2} sin θ d θ) (\int_{0}^{2} r^{2} d r) (\int_{0}^{4} z d z) = ({− cos θ |}_{0}^{π / 2}) ({\frac{r^{3}}{3} |}_{0}^{2}) ({\frac{z^{2}}{2} |}_{0}^{4}) = \frac{64}{3} . \end{matrix}

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	2 Timeshare 2 By Jams Kalo Start Quiz
	Engineering Communication MCQ By Steve Gibbs Start Quiz
	PE Power Enigeering Safety By Gerr Zen Start Quiz
©flickr: Derek	Treatment Of Psychological Disorders By Michael Nelson Start Quiz
	4 Practice Neuroanatomy MCQ Exam By David Corey Start Exam
©flickr:	Core Java Unit Test-1(CAJ003) By Abishek Devaraj Start Quiz
	13 Lec:13 Hypothesis Testing P-values By Janet Forrester Start Quiz
	10 Physiotherapy Modalities-Thermo By Rhodes Start Quiz
	Microeconomics Test 1 By IES Portal Start Test
	Business Law Ethics By Kevin Moquin Start Quiz