| << Chapter < Page | Chapter >> Page > |
Examples of gravitational orbits abound. Hundreds of artificial satellites orbit Earth together with thousands of pieces of debris. The Moon’s orbit about Earth has intrigued humans from time immemorial. The orbits of planets, asteroids, meteors, and comets about the Sun are no less interesting. If we look further, we see almost unimaginable numbers of stars, galaxies, and other celestial objects orbiting one another and interacting through gravity.
All these motions are governed by gravitational force, and it is possible to describe them to various degrees of precision. Precise descriptions of complex systems must be made with large computers. However, we can describe an important class of orbits without the use of computers, and we shall find it instructive to study them. These orbits have the following characteristics:
The conditions are satisfied, to good approximation, by Earth’s satellites (including the Moon), by objects orbiting the Sun, and by the satellites of other planets. Historically, planets were studied first, and there is a classical set of three laws, called Kepler’s laws of planetary motion, that describe the orbits of all bodies satisfying the two previous conditions (not just planets in our solar system). These descriptive laws are named for the German astronomer Johannes Kepler (1571–1630), who devised them after careful study (over some 20 years) of a large amount of meticulously recorded observations of planetary motion done by Tycho Brahe (1546–1601). Such careful collection and detailed recording of methods and data are hallmarks of good science. Data constitute the evidence from which new interpretations and meanings can be constructed.
Kepler’s First Law
The orbit of each planet about the Sun is an ellipse with the Sun at one focus.
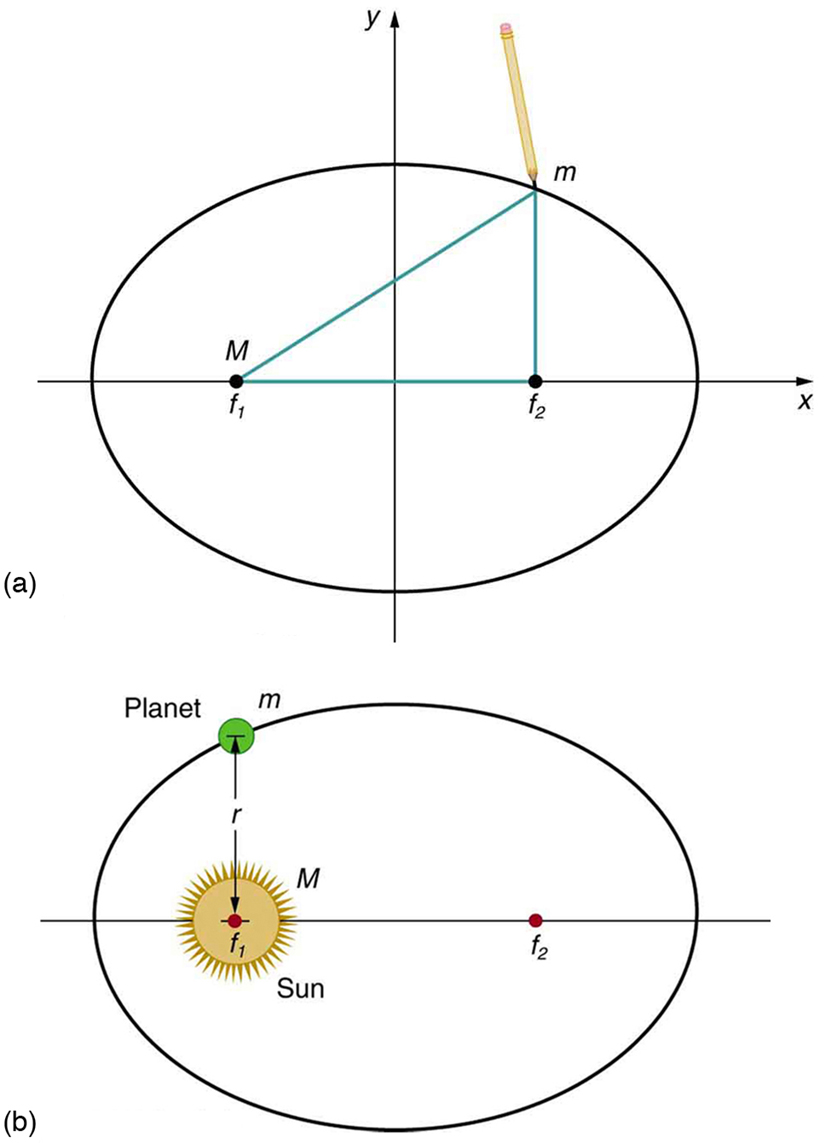
Kepler’s Second Law
Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times (see [link] ).

Notification Switch
Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?