| << Chapter < Page | Chapter >> Page > |
In the following exercises, convert the integrals to polar coordinates and evaluate them.
Evaluate the integral where is the region bounded by the polar axis and the upper half of the cardioid
Find the area of the region bounded by the polar axis and the upper half of the cardioid
Evaluate the integral where is the region bounded by the part of the four-leaved rose situated in the first quadrant (see the following figure).
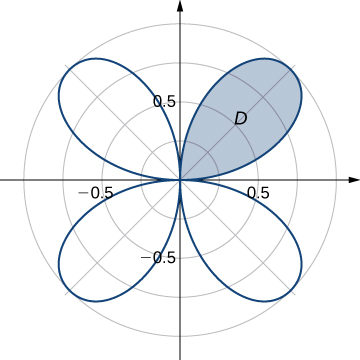
Find the total area of the region enclosed by the four-leaved rose (see the figure in the previous exercise).
Find the area of the region which is the region bounded by and
Find the area of the region which is the region inside the disk and to the right of the line
Determine the average value of the function over the region bounded by the polar curve where (see the following graph).
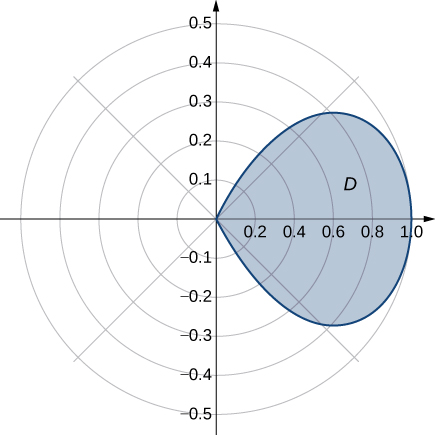
Determine the average value of the function over the region bounded by the polar curve where (see the following graph).
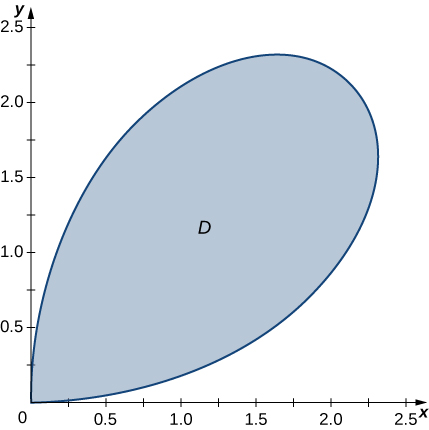
Find the volume of the solid situated in the first octant and bounded by the paraboloid and the planes and
Find the volume of the solid bounded by the paraboloid and the plane
a. b. c.
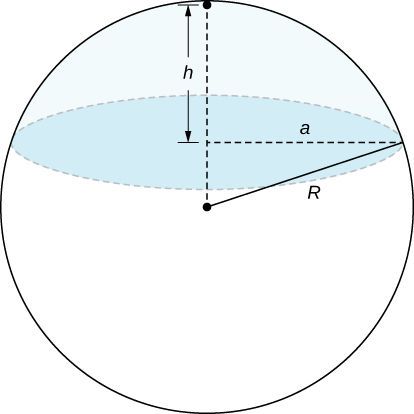
For the following two exercises, consider a spherical ring, which is a sphere with a cylindrical hole cut so that the axis of the cylinder passes through the center of the sphere (see the following figure).

If the sphere has radius and the cylinder has radius find the volume of the spherical ring.
A cylindrical hole of diameter cm is bored through a sphere of radius cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.
Find the volume of the solid that lies under the double cone inside the cylinder and above the plane
Find the volume of the solid that lies under the paraboloid inside the cylinder and above the plane
Find the volume of the solid that lies under the plane and above the disk
Find the volume of the solid that lies under the plane and above the unit disk
A radial function is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, where Show that if is a continuous radial function, then where and with and
Use the information from the preceding exercise to calculate the integral where is the unit disk.
Let be a continuous radial function defined on the annular region where and is a differentiable function. Show that
Apply the preceding exercise to calculate the integral where is the annular region between the circles of radii and situated in the third quadrant.
Let be a continuous function that can be expressed in polar coordinates as a function of only; that is, where with and Show that where is an antiderivative of
Apply the preceding exercise to calculate the integral where
Let be a continuous function that can be expressed in polar coordinates as a function of only; that is, where with and Show that where and are antiderivatives of and respectively.
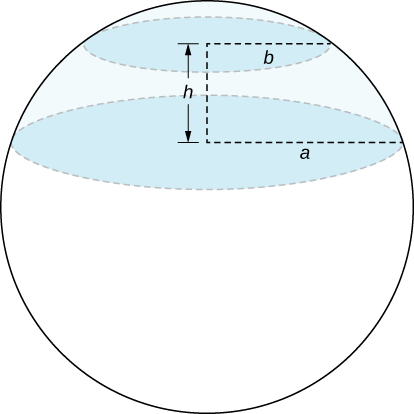
A spherical cap is the region of a sphere that lies above or below a given plane.
In statistics, the joint density for two independent, normally distributed events with a mean and a standard distribution is defined by Consider the Cartesian coordinates of a ball in the resting position after it was released from a position on the z -axis toward the -plane. Assume that the coordinates of the ball are independently normally distributed with a mean and a standard deviation of (in feet). The probability that the ball will stop no more than feet from the origin is given by where is the disk of radius a centered at the origin. Show that
The double improper integral may be defined as the limit value of the double integrals over disks of radii a centered at the origin, as a increases without bound; that is,

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?