5.3 Double integrals in polar coordinates  (Page 4/7)

The region $D$ for the integration is the base of the cone, which appears to be a circle on the $xy\text{-plane}$ (see the following figure).

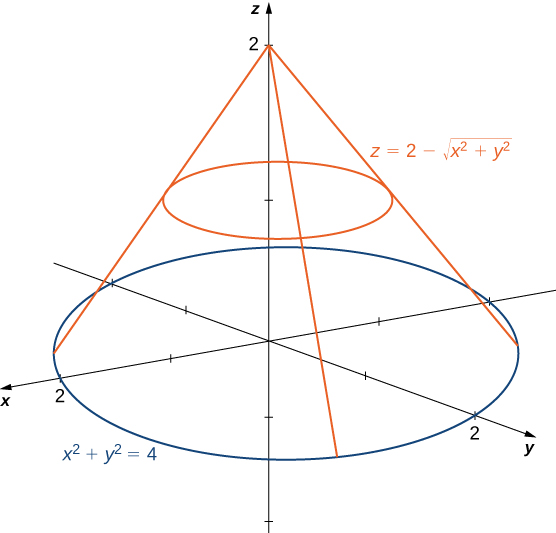
We find the equation of the circle by setting $z=0\text{:}$

This means the radius of the circle is $2,$ so for the integration we have $0\le \theta \le 2\pi$ and $0\le r\le 2.$ Substituting $x=r\text{cos}\theta$ and $y=r\text{sin}\theta$ in the equation $z=2-\sqrt{x^2+y^2}$ we have $z=2-r.$ Therefore, the volume of the cone is

${\displaystyle \underset{\theta =0}{\overset{\theta =2\pi }{\int }}{\displaystyle \underset{r=0}{\overset{r=2}{\int }}\left(2-r\right)}}rdrd\theta =2\pi \frac{4}{3}=\frac{8\pi }{3}$ cubic units.

Sketching the graph of the function $r=\text{cos}4\theta$ reveals that it is a polar rose with eight petals (see the following figure).

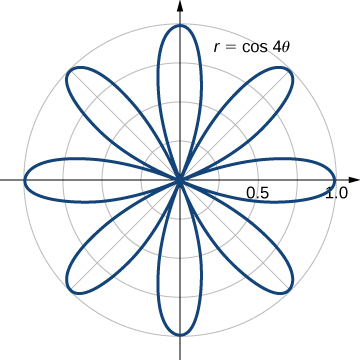
Using symmetry , we can see that we need to find the area of one petal and then multiply it by $8.$ Notice that the values of $\theta$ for which the graph passes through the origin are the zeros of the function $\text{cos}4\theta ,$ and these are odd multiples of $\pi \text{/}8.$ Thus, one of the petals corresponds to the values of $\theta$ in the interval $\left[\text{−}\pi \text{/}8,\pi \text{/}8\right].$ Therefore, the area bounded by the curve $r=\text{cos}4\theta$ is

First and foremost, sketch the graphs of the region ( [link] ).

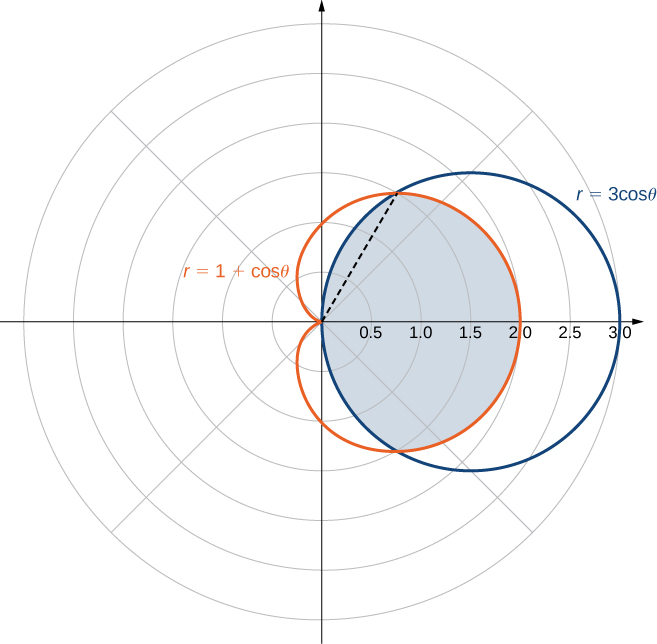
We can from see the symmetry of the graph that we need to find the points of intersection. Setting the two equations equal to each other gives

One of the points of intersection is $\theta =\pi \text{/}3.$ The area above the polar axis consists of two parts, with one part defined by the cardioid from $\theta =0$ to $\theta =\pi \text{/}3$ and the other part defined by the circle from $\theta =\pi \text{/}3$ to $\theta =\pi \text{/}2.$ By symmetry, the total area is twice the area above the polar axis. Thus, we have

Evaluating each piece separately, we find that the area is