| << Chapter < Page | Chapter >> Page > |
It has been stated that about 41% of adult workers have a high school diploma but do not pursue any further education. If 20 adult workers are randomly selected,
Let X = the number of workers who have a high school diploma but do not pursue any further education.
X takes on the values 0, 1, 2, ..., 20 where n = 20, p = 0.41, and q = 1 – 0.41 = 0.59. X ~ B (20, 0.41)
Go into 2 nd DISTR. The syntax for the instructions are as follows:
To calculate (
x = value): binompdf(
n ,
p , number) if "number" is left out, the result is the binomial probability table.
To calculate
P (
x ≤ value): binomcdf(
n ,
p , number) if "number" is left out, the result is the cumulative binomial probability table.
For this problem: After you are in 2
nd DISTR, arrow down to binomcdf. Press ENTER. Enter 20,0.41,12). The result is
P (
x ≤ 12) = 0.9738.
If you want to find P ( x = 12), use the pdf (binompdf). If you want to find P ( x >12), use 1 - binomcdf(20,0.41,12).
The probability that at most 12 workers have a high school diploma but do not pursue any further education is 0.9738.
The graph of X ~ B (20, 0.41) is as follows:
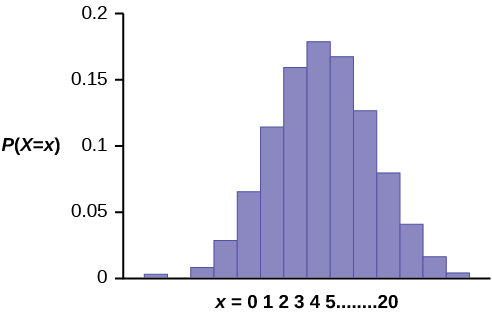
The y -axis contains the probability of X , where X = the number of workers who have only a high school diploma.
c. The number of adult workers that you expect to have a high school diploma but not pursue any further education is the mean, μ = np = (20)(0.41) = 8.2.
The formula for the variance is σ
2 =
npq . The standard deviation is
σ =
.
σ =
= 2.20.
About 32% of students participate in a community volunteer program outside of school. If 30 students are selected at random,
In the 2013 Jerry’s Artarama art supplies catalog, there are 560 pages. Eight of the pages feature signature artists. Suppose we randomly sample 100 pages. Let X = the number of pages that feature signature artists.

Notification Switch
Would you like to follow the 'Introduction to statistics i - stat 213 - university of calgary - ver2015revb' conversation and receive update notifications?