| << Chapter < Page | Chapter >> Page > |
Uniform : Suppose the time it takes a nine-year old to eat a donut is between 0.5 and 4 minutes, inclusive. Let = the time, in minutes, it takes a nine-year old child to eat a donut. Then ~ .
The probability that a randomly selected nine-year old child eats a donut in at least two minutes is _______.
0.5714
Find the probability that a different nine-year old child eats a donut in more than 2 minutes given that the child has already been eating the donut for more than 1.5 minutes.
The second probability question has a conditional (refer to " Probability Topics "). You are asked to find the probability that a nine-year old child eats a donut in more than 2 minutes given that the child has already been eating the donut for more than 1.5 minutes. Solve the problem two different ways (see the first example ). You must reduce the sample space. First way : Since you already know the child has already been eating the donut for more than 1.5 minutes, you are no longer starting at minutes. Your starting point is 1.5 minutes.
Write a new f(x):
for .
Find . Draw a graph.
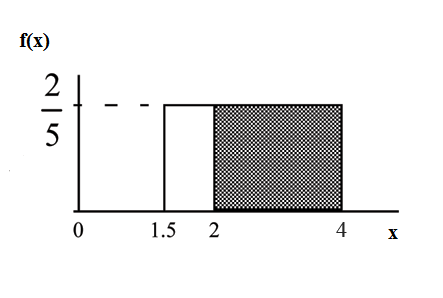
The probability that a nine-year old child eats a donut in more than 2 minutes given that the child has already been eating the donut for more than 1.5 minutes is .
Second way: Draw the original graph for ~ . Use the conditional formula
Uniform : Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and 4 hours. Let = the time needed to fix a furnace. Then ~ .
Find the probability that a randomly selected furnace repair requires longer than 2 hours.
To find : so
P(x>2) = (base)(height) = (4 − 2)(0.4) = 0.8
Example 4 figure 1

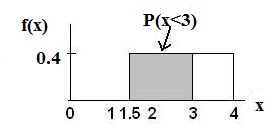
Find the probability that a randomly selected furnace repair requires less than 3 hours. Describe how the graph differs from the graph in the first part of this example.
= (base)(height) = (3 − 1.5)(0.4) = 0.6
The graph of the rectangle showing the entire distribution would remain the same. However the graph should be shaded between x=1.5 and x=3. Note that the shaded area starts at x=1.5 rather than at x=0; since X~U(1.5,4), x can not be less than 1.5.
Example 4 figure 2
Find the 30th percentile of furnace repair times.
Example 4 figure 3

The 30th percentile of repair times is 2.25 hours. 30% of repair times are 2.5 hours or less.
The longest 25% of furnace repair times take at least how long? (Find the minimum time for the longest 25% of repairs.)
Example 4 figure 4

The longest 25% of furnace repairs take at least 3.375 hours (3.375 hours or longer).
Note: Since 25% of repair times are 3.375 hours or longer, that means that 75% of repair times are 3.375 hours or less. 3.375 hours is the 75th percentile of furnace repair times.
**Example 5 contributed by Roberta Bloom

Notification Switch
Would you like to follow the 'Collaborative statistics' conversation and receive update notifications?