| << Chapter < Page | Chapter >> Page > |
We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:
In this section, we will see another way to define trigonometric functions using properties of right triangles .
In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of is its value at radians. First, we need to create our right triangle. [link] shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point to the x -axis, we have a right triangle whose vertical side has length and whose horizontal side has length We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

We know
Likewise, we know
These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of we will call the side between the given angle and the right angle the adjacent side to angle (Adjacent means “next to.”) Instead of we will call the side most distant from the given angle the opposite side from angle And instead of we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in [link] .
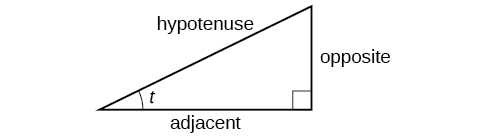
Given a right triangle with an acute angle of
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”
Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle.
Given the triangle shown in [link] , find the value of

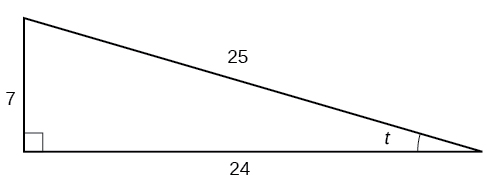
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so:
Given the triangle shown in [link] , find the value of

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?