1. Home
  2. Calculus volume 2
  3. Sequences and series
  4. Infinite series

5.2 Infinite series  (Page 2/16)

<< Chapter < Page
  Calculus volume 2     Page 2 / 16
Chapter >> Page >
S 1 = 1 S 2 = 1 + 1 2 = 3 2 S 3 = 1 + 1 2 + 1 4 = 7 4 S 4 = 1 + 1 2 + 1 4 + 1 8 = 15 8 S 5 = 1 + 1 2 + 1 4 + 1 8 + 1 16 = 31 16 .

Plotting some of these values in [link] , it appears that the sequence { S k } could be approaching 2.

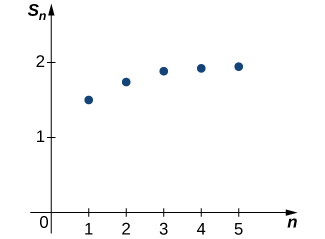
This is a graph in quadrant 1with the x and y axes labeled n and S_n, respectively. From 1 to 5, points are plotted. They increase and seem to converge to 2 and n goes to infinity.
The graph shows the sequence of partial sums { S k } . It appears that the sequence is approaching the value 2 .

Let’s look for more convincing evidence. In the following table, we list the values of S k for several values of k .

k 5 10 15 20
S k 1.9375 1.998 1.999939 1.999998

These data supply more evidence suggesting that the sequence { S k } converges to 2 . Later we will provide an analytic argument that can be used to prove that lim k → ∞ S k = 2 . For now, we rely on the numerical and graphical data to convince ourselves that the sequence of partial sums does actually converge to 2 . Since this sequence of partial sums converges to 2 , we say the infinite series converges to 2 and write

∑ n = 1 ∞ ( 1 2 ) n − 1 = 2 .

Returning to the question about the oil in the lake, since this infinite series converges to 2 , we conclude that the amount of oil in the lake will get arbitrarily close to 2000 gallons as the amount of time gets sufficiently large.

This series is an example of a geometric series. We discuss geometric series in more detail later in this section. First, we summarize what it means for an infinite series to converge.

Definition

An infinite series    is an expression of the form

∑ n = 1 ∞ a n = a 1 + a 2 + a 3 + ⋯ .

For each positive integer k , the sum

S k = ∑ n = 1 k a n = a 1 + a 2 + a 3 + ⋯ + a k

is called the k th partial sum    of the infinite series. The partial sums form a sequence { S k } . If the sequence of partial sums converges to a real number S , the infinite series converges. If we can describe the convergence of a series    to S , we call S the sum of the series, and we write

∑ n = 1 ∞ a n = S .

If the sequence of partial sums diverges, we have the divergence of a series    .

This website shows a more whimsical approach to series.

Note that the index for a series need not begin with n = 1 but can begin with any value. For example, the series

∑ n = 1 ∞ ( 1 2 ) n − 1

can also be written as

∑ n = 0 ∞ ( 1 2 ) n or ∑ n = 5 ∞ ( 1 2 ) n − 5 .

Often it is convenient for the index to begin at 1 , so if for some reason it begins at a different value, we can reindex by making a change of variables. For example, consider the series

∑ n = 2 ∞ 1 n 2 .

By introducing the variable m = n − 1 , so that n = m + 1 , we can rewrite the series as

∑ m = 1 ∞ 1 ( m + 1 ) 2 .

Evaluating limits of sequences of partial sums

For each of the following series, use the sequence of partial sums to determine whether the series converges or diverges.

  1. ∑ n = 1 ∞ n n + 1
  2. ∑ n = 1 ∞ ( −1 ) n
  3. ∑ n = 1 ∞ 1 n ( n + 1 )
  1. The sequence of partial sums { S k } satisfies
    S 1 = 1 2 S 2 = 1 2 + 2 3 S 3 = 1 2 + 2 3 + 3 4 S 4 = 1 2 + 2 3 + 3 4 + 4 5 .

    Notice that each term added is greater than 1 / 2 . As a result, we see that
    S 1 = 1 2 S 2 = 1 2 + 2 3 > 1 2 + 1 2 = 2 ( 1 2 ) S 3 = 1 2 + 2 3 + 3 4 > 1 2 + 1 2 + 1 2 = 3 ( 1 2 ) S 4 = 1 2 + 2 3 + 3 4 + 4 5 > 1 2 + 1 2 + 1 2 + 1 2 = 4 ( 1 2 ) .

    From this pattern we can see that S k > k ( 1 2 ) for every integer k . Therefore, { S k } is unbounded and consequently, diverges. Therefore, the infinite series ∑ n = 1 ∞ n / ( n + 1 ) diverges.
  2. The sequence of partial sums { S k } satisfies
    S 1 = −1 S 2 = −1 + 1 = 0 S 3 = −1 + 1 − 1 = −1 S 4 = −1 + 1 − 1 + 1 = 0 .

    From this pattern we can see the sequence of partial sums is
    { S k } = { −1 , 0 , −1 , 0 ,… } .

    Since this sequence diverges, the infinite series ∑ n = 1 ∞ ( −1 ) n diverges.
  3. The sequence of partial sums { S k } satisfies
    S 1 = 1 1 · 2 = 1 2 S 2 = 1 1 · 2 + 1 2 · 3 = 1 2 + 1 6 = 2 3 S 3 = 1 1 · 2 + 1 2 · 3 + 1 3 · 4 = 1 2 + 1 6 + 1 12 = 3 4 S 4 = 1 1 · 2 + 1 2 · 3 + 1 3 · 4 + 1 4 · 5 = 4 5 S 5 = 1 1 · 2 + 1 2 · 3 + 1 3 · 4 + 1 4 · 5 + 1 5 · 6 = 5 6 .

    From this pattern, we can see that the k th partial sum is given by the explicit formula
    S k = k k + 1 .

    Since k / ( k + 1 ) → 1 , we conclude that the sequence of partial sums converges, and therefore the infinite series converges to 1 . We have
    ∑ n = 1 ∞ 1 n ( n + 1 ) = 1 .
Got questions? Get instant answers now!
Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 2. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11965/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?

Ask