4.7 Maxima/minima problems  (Page 6/10)

Using the problem-solving strategy, step $1$ involves finding the critical points of $f$ on its domain. Therefore, we first calculate $f_x\left(x,y\right)$ and $f_y\left(x,y\right),$ then set them each equal to zero:

Setting them equal to zero yields the system of equations

The solution to this system is $x=21$ and $y=3.$ Therefore $\left(21,3\right)$ is a critical point of $f.$ Calculating $f\left(21,3\right)$ gives $f\left(21,3\right)=48\left(21\right)+96\left(3\right)-{21}^2-2\left(21\right)\left(3\right)-9{\left(3\right)}^2=648.$

The domain of this function is $0\le x\le 50$ and $0\le y\le 25$ as shown in the following graph.

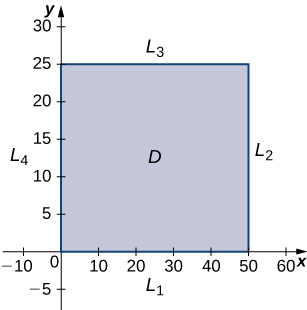
$L_1$ is the line segment connecting $\left(0,0\right)$ and $\left(50,0\right),$ and it can be parameterized by the equations $x\left(t\right)=t,y\left(t\right)=0$ for $0\le t\le 50.$ We then define $g\left(t\right)=f\left(x\left(t\right),y\left(t\right)\right)\text{:}$

Setting $g^{\prime }\left(t\right)=0$ yields the critical point $t=24,$ which corresponds to the point $\left(24,0\right)$ in the domain of $f.$ Calculating $f\left(24,0\right)$ gives $576.$

$L_2$ is the line segment connecting $$ and $\left(50,25\right),$ and it can be parameterized by the equations $x\left(t\right)=50,y\left(t\right)=t$ for $0\le t\le 25.$ Once again, we define $g\left(t\right)=f\left(x\left(t\right),y\left(t\right)\right)\text{:}$

This function has a critical point at $t=-\frac{2}{9},$ which corresponds to the point $\left(50,-\frac{2}{9}\right).$ This point is not in the domain of $f.$

$L_3$ is the line segment connecting $\left(0,25\right)\text{and}\left(50,25\right),$ and it can be parameterized by the equations $x\left(t\right)=t,y\left(t\right)=25$ for $0\le t\le 50.$ We define $g\left(t\right)=f\left(x\left(t\right),y\left(t\right)\right)\text{:}$

This function has a critical point at $t=\mathrm{-1},$ which corresponds to the point $\left(\mathrm{-1},25\right),$ which is not in the domain.

$L_4$ is the line segment connecting $\left(0,0\right)\text{to}\left(0,25\right),$ and it can be parameterized by the equations $x\left(t\right)=0,y\left(t\right)=t$ for $0\le t\le 25.$ We define $g\left(t\right)=f\left(x\left(t\right),y\left(t\right)\right)\text{:}$

This function has a critical point at $t=\frac{16}{3},$ which corresponds to the point $\left(0,\frac{16}{3}\right),$ which is on the boundary of the domain. Calculating $f\left(0,\frac{16}{3}\right)$ gives $256.$

We also need to find the values of $f\left(x,y\right)$ at the corners of its domain. These corners are located at $\left(0,0\right),\left(50,0\right),\left(50,25\right)\text{and}\left(0,25\right)\text{:}$

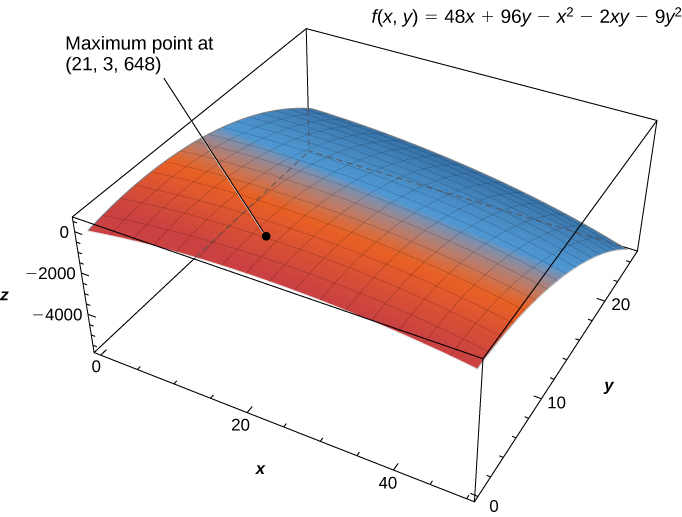
The maximum critical value is $648,$ which occurs at $\left(21,3\right).$ Therefore, a maximum profit of $\text{\$}\mathrm{648,000}$ is realized when $\mathrm{21,000}$ golf balls are sold and $3$ hours of advertising are purchased per month as shown in the following figure.