4.6 Phasors: light scattering by a slit

One of the most spectacular successes for phasor analysis arises in the study of light diffraction by a narrow slit. The experiment is to shine laserlight through a slit in an otherwise opaque sheet and observe the pattern of light that falls on a distant screen. When the slit is very narrow comparedwith the wavelength of the light, then the light that falls on the screen is nearly uniform in intensity. However, when the width of the slit is comparable to thewavelength of the light, the pattern of light that falls on the screen is scalloped in intensity, showing alternating light and dark bands. The experiment, andthe observed results, are illustrated in [link] .

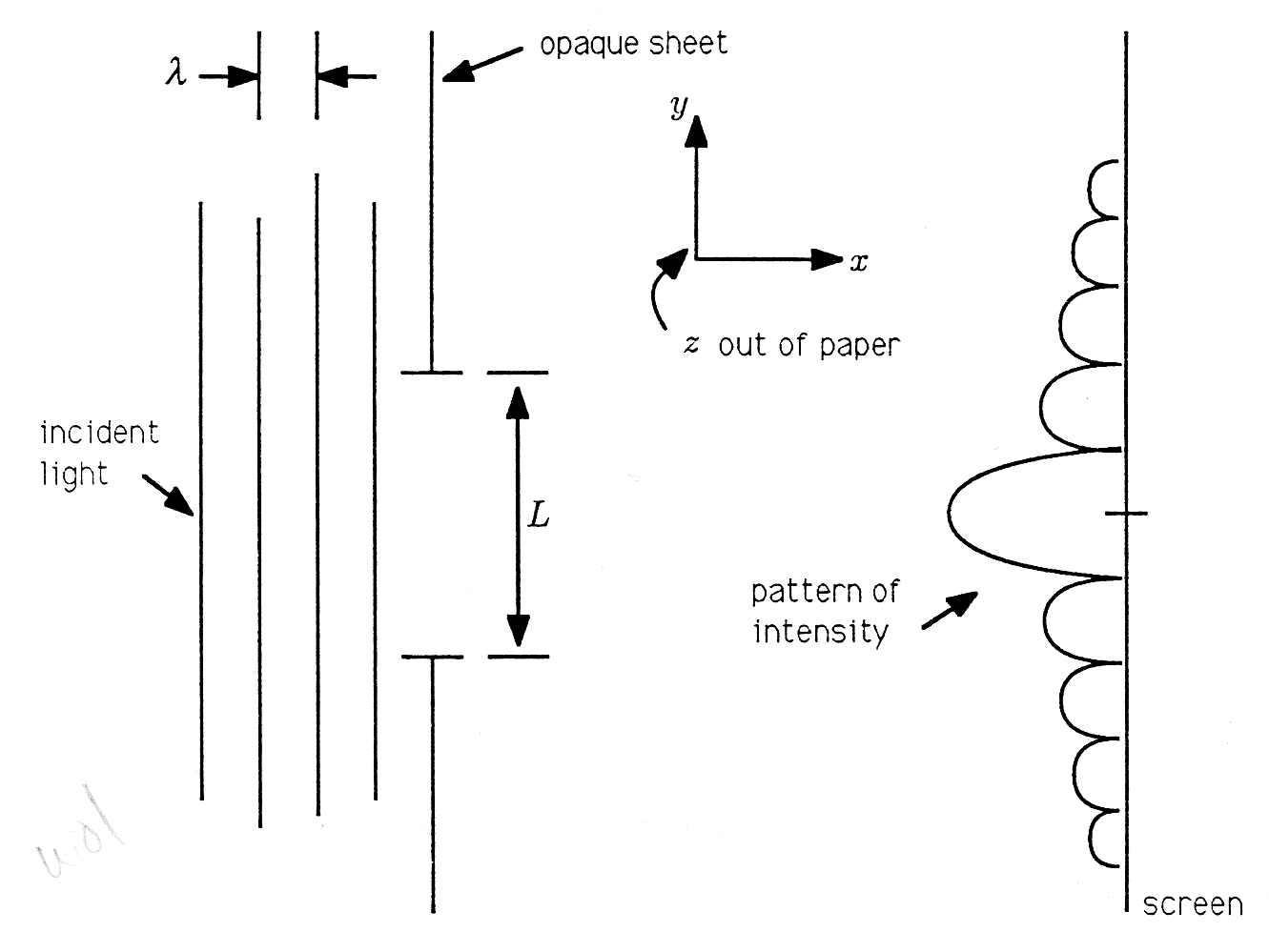
Why should this experiment produce this result? Phasor analysis illuminates the question and produces an elegant mathematical description of a profoundly important optical experiment.

Huygens's Principle. We will assume, as Christiaan Huygens did, that the light incident on the slit sets up a light field in the slit that may be modeled by $N$ discrete sources, each of which radiates a “spherical wave of light.” This model is illustrated in [link] . The distance between sources is $d$ , and $Nd=L$ is the width of the slit. Each source is indexed by $n$ , and $n$ runs from 0 to $N-1$ . The $0^{th}$ source is located at the origin of our coordinate system.

The spherical wave radiated by the $n^{th}$ source is described by the equation

The function $E(r_n,t)$ describes the “electric field” at time t and distance r _n from the $n^{th}$ source. The field is constant as long as the variable $\omega t-(2\pi /\lambda )r_n$ is constant. Therefore, if we freeze time at $t=t_0$ , the field will be constant on a sphere of radius $r_n$ . This is illustrated in [link] .

Geometry. If we now pick a point $P$ on a distant screen, that point will be at distance $r_0$ from source $0,...,r_n$ from source $n,...$ , and so on. If we isolate the sources 0 and $n$ , then we have the geometric picture of [link] . The angle $\phi$ is the angle that point $P$ makes with the horizontal axis. The Pythagorean theorem says that the connection between distances $r_0$ and $r_n$ is

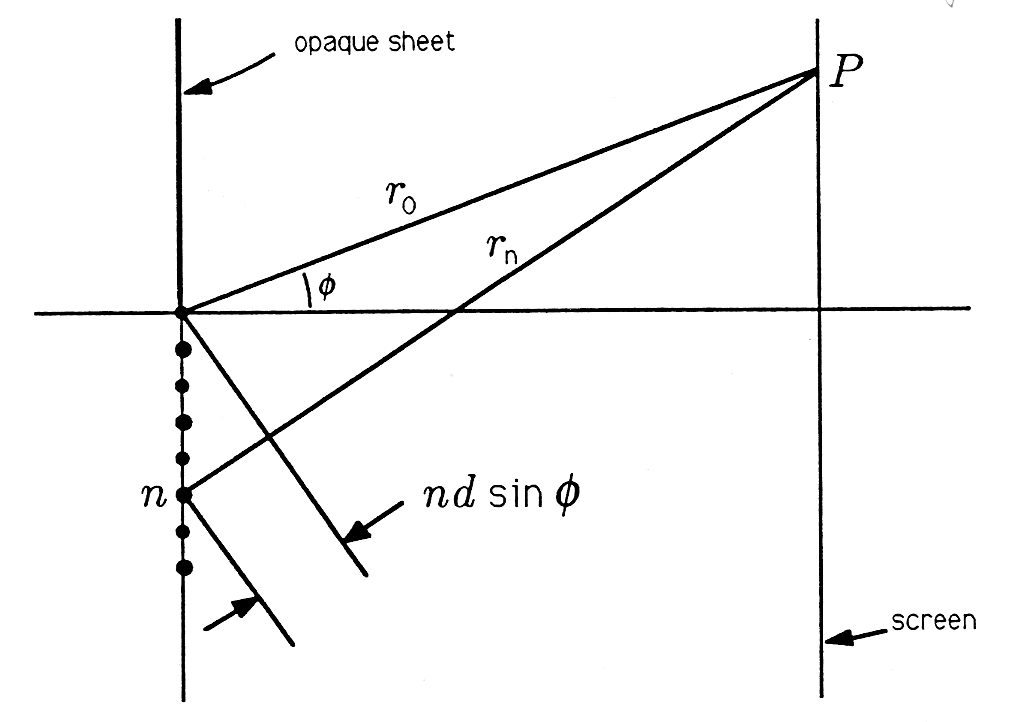
Let's try the solution

This solution produces the approximate identity

This will be close for $\frac{nd}{r_0}<<1$ . We will assume that the slit width $L$ is small compared to the distance to any point on the screen. Then $\frac{Nd}{r_0}=\frac{L}{r_0}<<1$ , in which case the approximate solution for $r_n$ is valid for all $n$ . This means that, for any point $P$ on the distant screen, the light contributed by the $n^{th}$ source is approximately

The phasor representation for this function is just

Note that $E_0\left(\phi \right)$ , the phasor associated with the $0^{th}$ source, is $\frac{A}{N}{e}^{-j(2\pi /\lambda )r_0}$ . Therefore we may write the phasor representation for the light contributed by the $n^{th}$ source to be

This result is very important because it shows the light arriving at point P from different sources to be “out of phase” by an amount that depends on the ratio $\frac{ndsin\phi }{\lambda }$

Phasors and Interference. The phasor representation for the field observed at point $P$ on the screen is the sum of the phasors contributed by each source:

This is a sum of the form

where the angle $\theta$ is $(2\pi /\lambda )dsin\phi$ . This sum is illustrated in [link] for several representative values of $\theta$ . Note that for small $\theta$ , meaning small $\phi$ , the sum has large magnitude, whereas for $\theta$ on the order of $2\pi /N$ , the sum is small. This simple geometric interpretation shows that for some values of $\phi$ , corresponding to some points $P$ on the screen, there will be constructive interference between the phasors, while for other values of $\phi$ there will be destructive interference. Constructive interference produces bright light, anddestructive interference produces darkness.

The geometry of [link] is illuminating. However, we already know from our study of complex numbers and geometric sums that the phasor sumof Equation 3.85 may be written as

This result may be manipulated to produce the form

The magnitude is the intensity of the light at angle φ from horizontal:

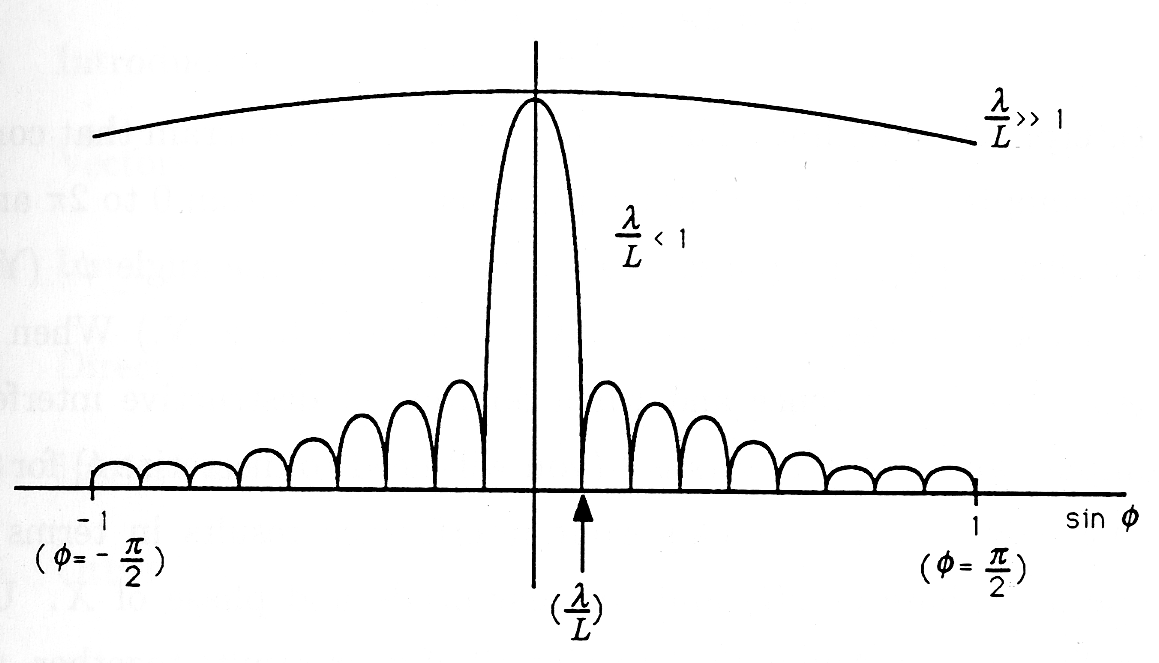
Limiting Form. Huygens's model is exact when $d$ shrinks to 0 and $N$ increases to infinity in such a way that $Nd\to L$ , the slit width. Then

This function is plotted in [link] for two values of $\frac{L}{\lambda }$ the width of the slit measured in wavelengths. When $\frac{L}{\lambda }<<1$ (i.e., $\frac{\lambda }{L}>>1$ ), then the light is uniformly distributed on the screen. However, when $\frac{L}{\lambda }>1(\frac{\lambda }{L}<1)$ , then the function has many zeros for $|$ sin $\phi |<1$ , as illustrated in the figure. These zeros correspond to dark spots on the screen where the fields radiated fromthe infinity of points within the slit interfere destructively.