| << Chapter < Page | Chapter >> Page > |
If you know the value of a single real sample and you know its position in the series relative to the origin, you can write equationsthat describe the real and imaginary parts of the transform of that single sample without any requirement to actually perform a Fourier transform.
Those equations are simple sine and cosine equations as a function of the units of the output domain. This is an important concept that contributesgreatly to the implementation of the FFT algorithm.
The FFT algorithm is an algorithm that transforms a series of complex values in one domain into a series of complex values in another domain. The images inthe figures discussed so far indicate a transformation of a complex function given by f(x) into another complex function given by F(k). There is nothing inthese images to indicate anything about time and frequency.
If the complex part of the input series f(x) is not zero, things get somewhat more complicated. For example, the real and imaginary parts of the transform ofan impulse having both real and imaginary parts are not necessarily cosine and sine curves. This is illustrated in Figure 8 .
| Figure 8. Transform of a complex impulse with a shift equal to two sample intervals. |
|---|
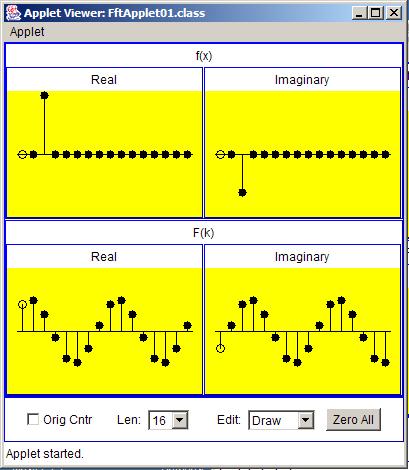 |
Figure 8 shows the results of transforming an impulse having both real andimaginary parts and a shift of two sample intervals.
Although both the real and imaginary parts of the transformed result have the shape of a sinusoid, neither is a cosine curve and neither is a sine curve. Bothof the curves are sinusoidal curves that have been shifted along the horizontal output axis moving their peaks and zero crossings away from the origin.
Because the Fourier transform is a linear transform, you can transform the real and imaginary parts of the input separately and add the two resultingtransforms. The sum of the two transforms represents the transform of the entire input series including both real and imaginary parts. The program that I willdiscuss later takes advantage of this fact. Once again, the main point is:
Even for a complex input series, if you know the values of the real and imaginary parts of a sample and you know the value of the shiftassociated with that sample, you can write equations that describe the real part and the imaginary part of the transform results.
That brings us to the crux of the matter. Given an input series consisting of a set of sequential samples taken atuniform sampling intervals, we know how to write equations for the real and imaginary parts that would be produced by performing a Fourier transform oneach of those samples individually.
We know that we can consider the input series to consist of the sum of the individual samples, each having a specified value and a different shift. We knowthat the Fourier transform is a linear transform. Therefore, the Fourier transform of an input series is the sum of the transforms of the individualsamples.

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?