| << Chapter < Page | Chapter >> Page > |
In the next example, one of the fractions has a variable in its numerator. We follow the same steps as when both numerators are numbers.
Add:
The fractions have different denominators.
Find the LCD.
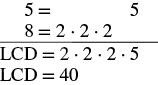 |
|
| Rewrite as equivalent fractions with the LCD. |
|
| Simplify the numerators and denominators. | |
| Add. |
We cannot add and since they are not like terms, so we cannot simplify the expression any further.
By now in this chapter, you have practiced multiplying, dividing, adding, and subtracting fractions. The following table summarizes these four fraction operations. Remember: You need a common denominator to add or subtract fractions, but not to multiply or divide fractions
Fraction multiplication: Multiply the numerators and multiply the denominators.
Fraction division: Multiply the first fraction by the reciprocal of the second.
Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
Simplify:
First we ask ourselves, “What is the operation?”
ⓐ The operation is addition.
Do the fractions have a common denominator? No.
Find the LCD.
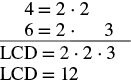 |
|
| Rewrite each fraction as an equivalent fraction with the LCD. |
|
| Simplify the numerators and denominators. | |
| Add the numerators and place the sum over the common denominator. | |
| Check to see if the answer can be simplified. It cannot. |
ⓑ The operation is division. We do not need a common denominator.
| To divide fractions, multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Simplify. |
Simplify:
ⓐ The operation is subtraction. The fractions do not have a common denominator.
| Rewrite each fraction as an equivalent fraction with the LCD, 30. | |
| Subtract the numerators and place the difference over the common denominator. |
ⓑ The operation is multiplication; no need for a common denominator.
| To multiply fractions, multiply the numerators and multiply the denominators. | |
| Rewrite, showing common factors. | |
| Remove common factors to simplify. |
In Multiply and Divide Mixed Numbers and Complex Fractions , we saw that a complex fraction is a fraction in which the numerator or denominator contains a fraction. We simplified complex fractions by rewriting them as division problems. For example,

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?