| << Chapter < Page | Chapter >> Page > |
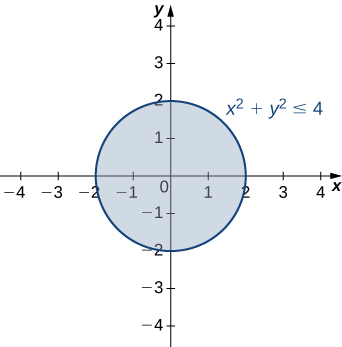
Find the domain and range of the function
The domain is the shaded circle defined by the inequality
which has a circle of radius
as its boundary. The range is
Suppose we wish to graph the function This function has two independent variables and one dependent variable When graphing a function of one variable, we use the Cartesian plane. We are able to graph any ordered pair in the plane, and every point in the plane has an ordered pair associated with it. With a function of two variables, each ordered pair in the domain of the function is mapped to a real number Therefore, the graph of the function consists of ordered triples The graph of a function of two variables is called a surface .
To understand more completely the concept of plotting a set of ordered triples to obtain a surface in three-dimensional space, imagine the coordinate system laying flat. Then, every point in the domain of the function has a unique associated with it. If is positive, then the graphed point is located above the if is negative, then the graphed point is located below the The set of all the graphed points becomes the two-dimensional surface that is the graph of the function
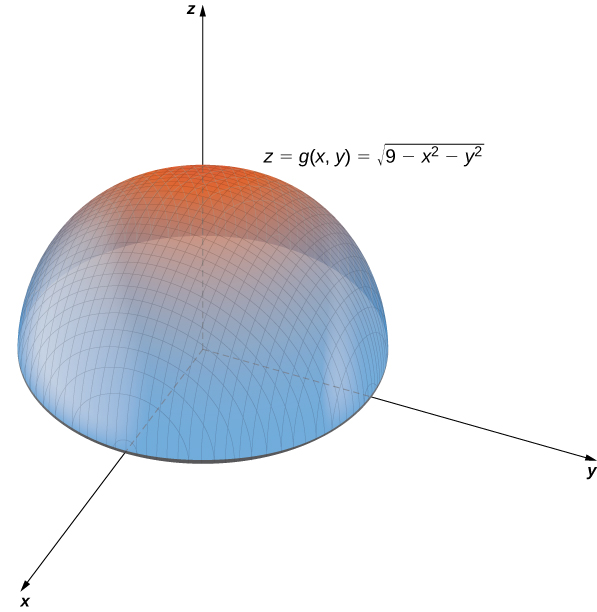
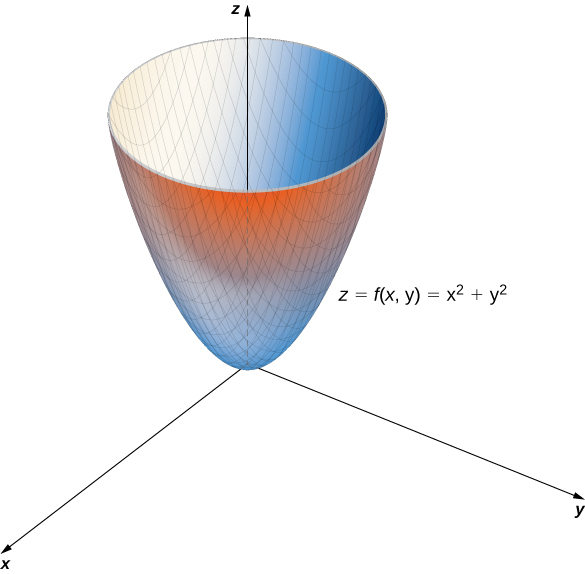
Create a graph of each of the following functions:
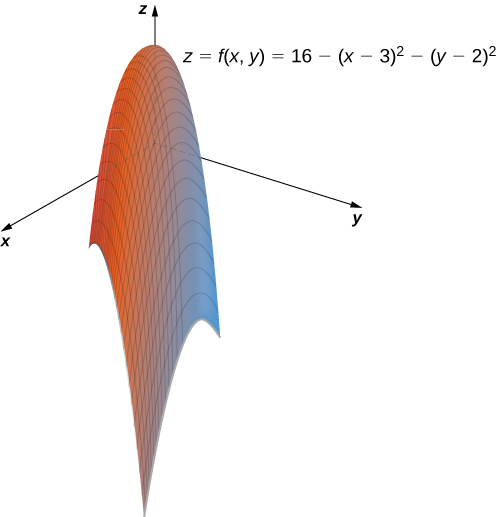
A profit function for a hardware manufacturer is given by
where is the number of nuts sold per month (measured in thousands) and represents the number of bolts sold per month (measured in thousands). Profit is measured in thousands of dollars. Sketch a graph of this function.
This function is a polynomial function in two variables. The domain of consists of coordinate pairs that yield a nonnegative profit:
This is a disk of radius centered at A further restriction is that both must be nonnegative. When and Note that it is possible for either value to be a noninteger; for example, it is possible to sell thousand nuts in a month. The domain, therefore, contains thousands of points, so we can consider all points within the disk. For any we can solve the equation
Since we know that so the previous equation describes a circle with radius centered at the point Therefore. the range of is The graph of is also a paraboloid, and this paraboloid points downward as shown.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?