| << Chapter < Page | Chapter >> Page > |
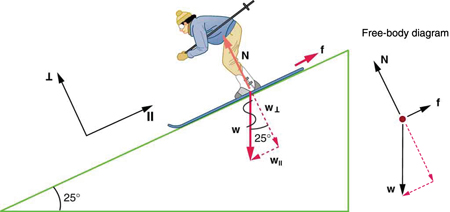
Consider the skier on a slope shown in [link] . Her mass including equipment is 60.0 kg. (a) What is her acceleration if friction is negligible? (b) What is her acceleration if friction is known to be 45.0 N?
Strategy
This is a two-dimensional problem, since the forces on the skier (the system of interest) are not parallel. The approach we have used in two-dimensional kinematics also works very well here. Choose a convenient coordinate system and project the vectors onto its axes, creating two connected one -dimensional problems to solve. The most convenient coordinate system for motion on an incline is one that has one coordinate parallel to the slope and one perpendicular to the slope. (Remember that motions along mutually perpendicular axes are independent.) We use the symbols and to represent perpendicular and parallel, respectively. This choice of axes simplifies this type of problem, because there is no motion perpendicular to the slope and because friction is always parallel to the surface between two objects. The only external forces acting on the system are the skier’s weight, friction, and the support of the slope, respectively labeled , , and in [link] . is always perpendicular to the slope, and is parallel to it. But is not in the direction of either axis, and so the first step we take is to project it into components along the chosen axes, defining to be the component of weight parallel to the slope and the component of weight perpendicular to the slope. Once this is done, we can consider the two separate problems of forces parallel to the slope and forces perpendicular to the slope.
Solution
The magnitude of the component of the weight parallel to the slope is , and the magnitude of the component of the weight perpendicular to the slope is .
(a) Neglecting friction. Since the acceleration is parallel to the slope, we need only consider forces parallel to the slope. (Forces perpendicular to the slope add to zero, since there is no acceleration in that direction.) The forces parallel to the slope are the amount of the skier’s weight parallel to the slope and friction . Using Newton’s second law, with subscripts to denote quantities parallel to the slope,
where , assuming no friction for this part, so that
is the acceleration.
(b) Including friction. We now have a given value for friction, and we know its direction is parallel to the slope and it opposes motion between surfaces in contact. So the net external force is now

Notification Switch
Would you like to follow the 'College physics arranged for cpslo phys141' conversation and receive update notifications?