| << Chapter < Page | Chapter >> Page > |
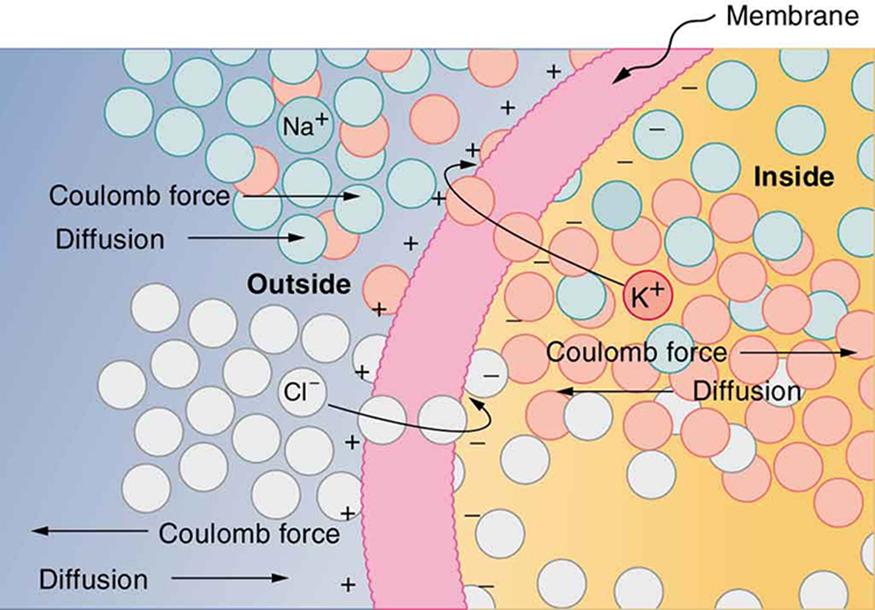
The separation of charge creates a potential difference of 70 to 90 mV across the cell membrane. While this is a small voltage, the resulting electric field ( ) across the only 8-nm-thick membrane is immense (on the order of 11 MV/m!) and has fundamental effects on its structure and permeability. Now, if the exterior of a neuron is taken to be at 0 V, then the interior has a resting potential of about –90 mV. Such voltages are created across the membranes of almost all types of animal cells but are largest in nerve and muscle cells. In fact, fully 25% of the energy used by cells goes toward creating and maintaining these potentials.
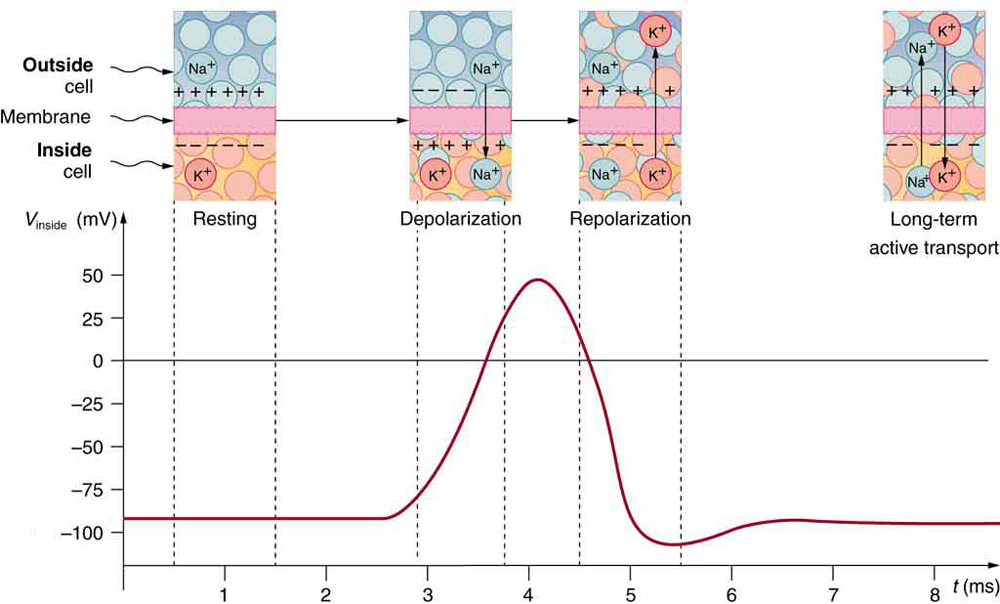
Electric currents along the cell membrane are created by any stimulus that changes the membrane’s permeability. The membrane thus temporarily becomes permeable to , which then rushes in, driven both by diffusion and the Coulomb force. This inrush of first neutralizes the inside membrane, or depolarizes it, and then makes it slightly positive. The depolarization causes the membrane to again become impermeable to , and the movement of quickly returns the cell to its resting potential, or repolarizes it. This sequence of events results in a voltage pulse, called the action potential . (See [link] .) Only small fractions of the ions move, so that the cell can fire many hundreds of times without depleting the excess concentrations of and . Eventually, the cell must replenish these ions to maintain the concentration differences that create bioelectricity. This sodium-potassium pump is an example of active transport , wherein cell energy is used to move ions across membranes against diffusion gradients and the Coulomb force.
The action potential is a voltage pulse at one location on a cell membrane. How does it get transmitted along the cell membrane, and in particular down an axon, as a nerve impulse? The answer is that the changing voltage and electric fields affect the permeability of the adjacent cell membrane, so that the same process takes place there. The adjacent membrane depolarizes, affecting the membrane further down, and so on, as illustrated in [link] . Thus the action potential stimulated at one location triggers a nerve impulse that moves slowly (about 1 m/s) along the cell membrane.

Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?