| << Chapter < Page | Chapter >> Page > |
Discussion
The numbers used in this example are reasonable for a moderately large barge. It is certainly difficult to obtain larger accelerations with tugboats, and small speeds are desirable to avoid running the barge into the docks. Drag is relatively small for a well-designed hull at low speeds, consistent with the answer to this example, where is less than 1/600th of the weight of the ship.
In the earlier example of a tightrope walker we noted that the tensions in wires supporting a mass were equal only because the angles on either side were equal. Consider the following example, where the angles are not equal; slightly more trigonometry is involved.
Consider the traffic light (mass 15.0 kg) suspended from two wires as shown in [link] . Find the tension in each wire, neglecting the masses of the wires.
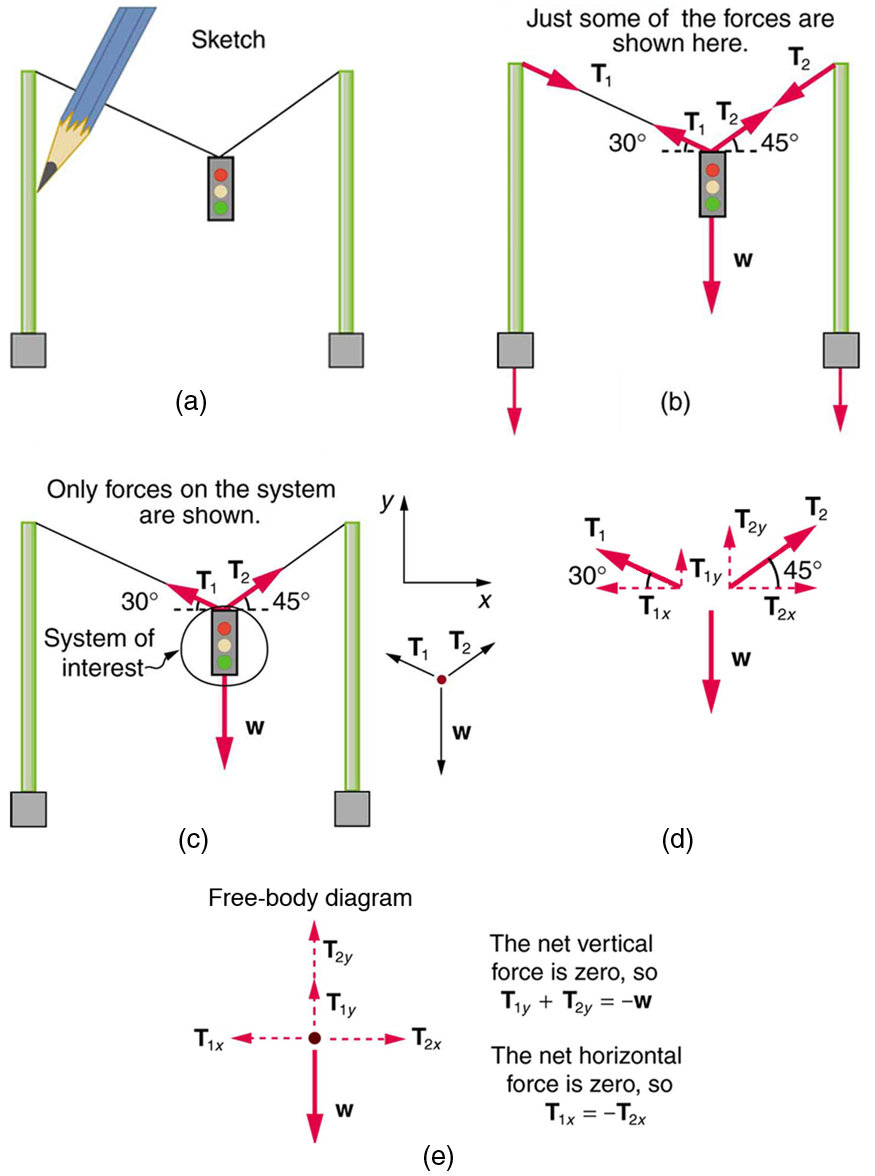
Strategy
The system of interest is the traffic light, and its free-body diagram is shown in [link] (c). The three forces involved are not parallel, and so they must be projected onto a coordinate system. The most convenient coordinate system has one axis vertical and one horizontal, and the vector projections on it are shown in part (d) of the figure. There are two unknowns in this problem ( and ), so two equations are needed to find them. These two equations come from applying Newton’s second law along the vertical and horizontal axes, noting that the net external force is zero along each axis because acceleration is zero.
Solution
First consider the horizontal or x -axis:
Thus, as you might expect,
This gives us the following relationship between and :
Thus,
Note that and are not equal in this case, because the angles on either side are not equal. It is reasonable that ends up being greater than , because it is exerted more vertically than .
Now consider the force components along the vertical or y -axis:
This implies
Substituting the expressions for the vertical components gives
There are two unknowns in this equation, but substituting the expression for in terms of reduces this to one equation with one unknown:
which yields
Solving this last equation gives the magnitude of to be
Finally, the magnitude of is determined using the relationship between them, = 1.225 , found above. Thus we obtain
Discussion
Both tensions would be larger if both wires were more horizontal, and they will be equal if and only if the angles on either side are the same (as they were in the earlier example of a tightrope walker).

Notification Switch
Would you like to follow the 'College physics: physics of california' conversation and receive update notifications?