| << Chapter < Page | Chapter >> Page > |
Local behavior:
End behavior:
Local behavior: End behavior:
Local behavior: ,
End behavior:
For the following exercises, find the slant asymptote of the functions.
For the following exercises, use the given transformation to graph the function. Note the vertical and horizontal asymptotes.
The reciprocal function shifted up two units.
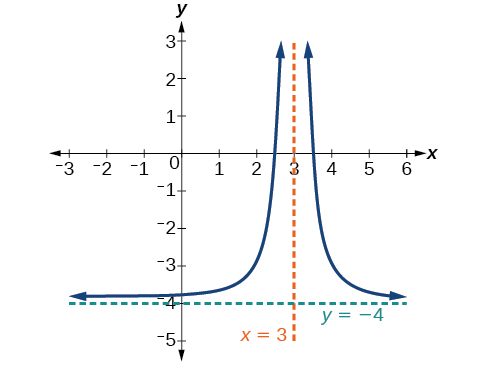
The reciprocal function shifted down one unit and left three units.
The reciprocal squared function shifted to the right 2 units.
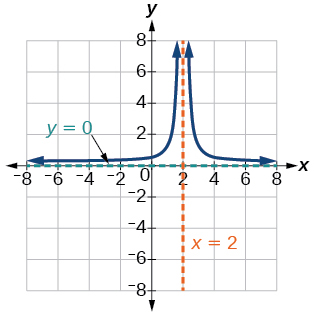
The reciprocal squared function shifted down 2 units and right 1 unit.
For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.
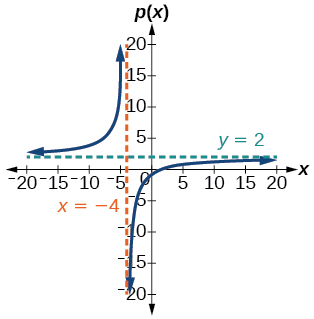
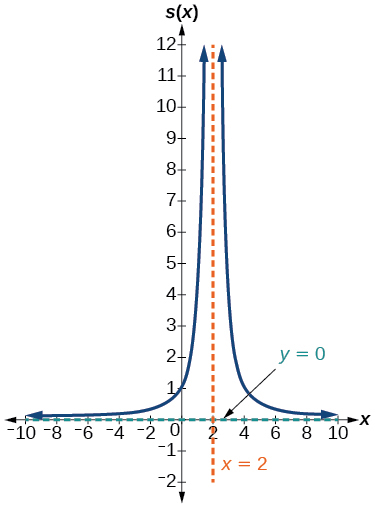
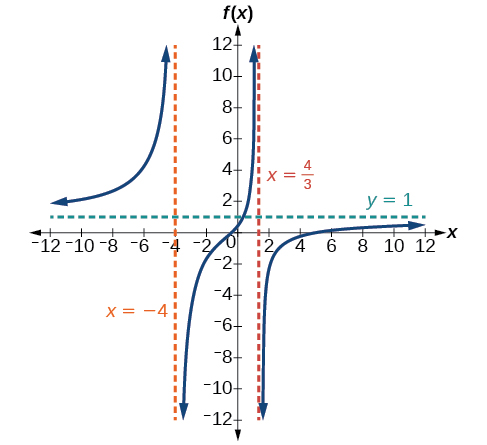
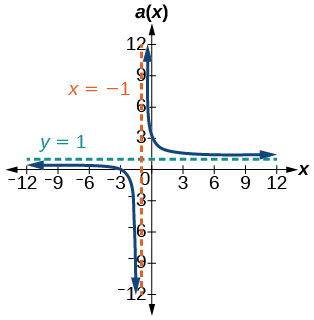
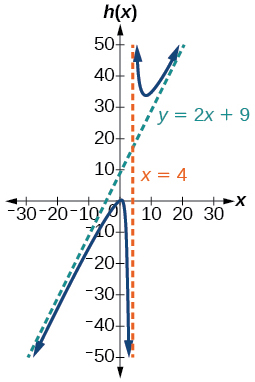
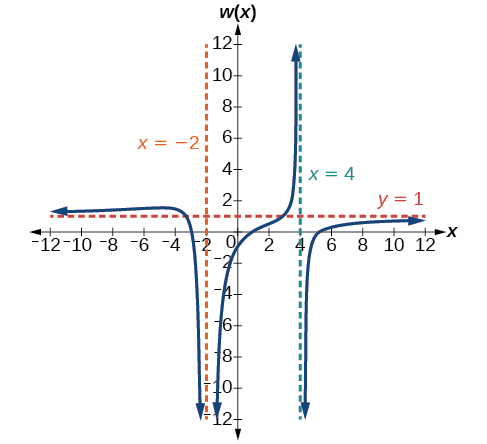
For the following exercises, write an equation for a rational function with the given characteristics.
Vertical asymptotes at and x -intercepts at and y -intercept at
Vertical asymptotes at and x- intercepts at and y- intercept at
Vertical asymptotes at and x -intercepts at and Horizontal asymptote at
Vertical asymptotes at and x -intercepts at and Horizontal asymptote at
Vertical asymptote at Double zero at y -intercept at
Vertical asymptote at Double zero at y -intercept at
For the following exercises, use the graphs to write an equation for the function.
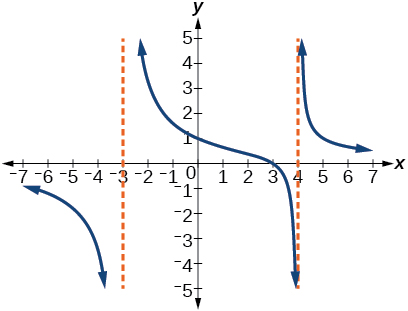
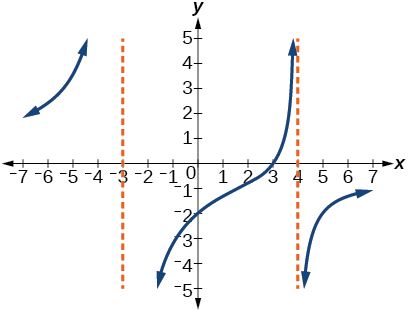
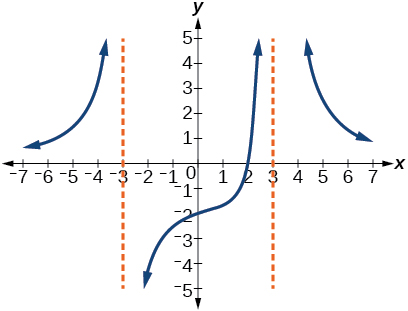
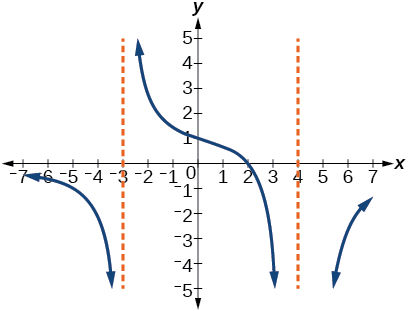
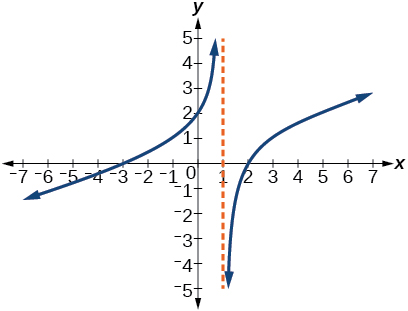
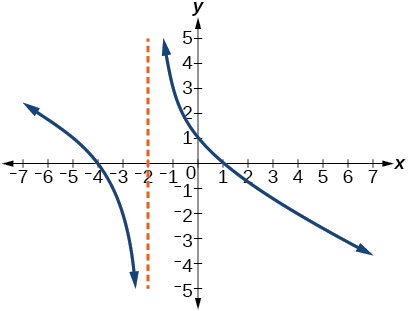

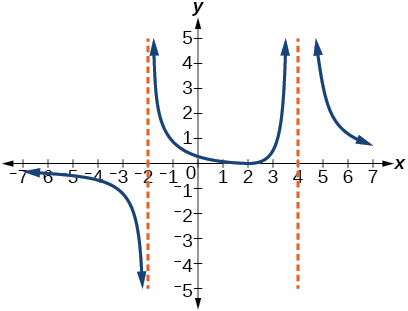
For the following exercises, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote
| 2.01 | 2.001 | 2.0001 | 1.99 | 1.999 | |
| 100 | 1,000 | 10,000 | –100 | –1,000 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
|---|---|---|---|---|---|
| .125 | .0102 | .001 | .0001 | .00001 |
Vertical asymptote Horizontal asymptote
| –4.1 | –4.01 | –4.001 | –3.99 | –3.999 | |
| 82 | 802 | 8,002 | –798 | –7998 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
| 1.4286 | 1.9331 | 1.992 | 1.9992 | 1.999992 |
Vertical asymptote Horizontal asymptote
| –.9 | –.99 | –.999 | –1.1 | –1.01 | |
| 81 | 9,801 | 998,001 | 121 | 10,201 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
| .82645 | .9803 | .998 | .9998 |
Vertical asymptote Horizontal asymptote
For the following exercises, use a calculator to graph Use the graph to solve
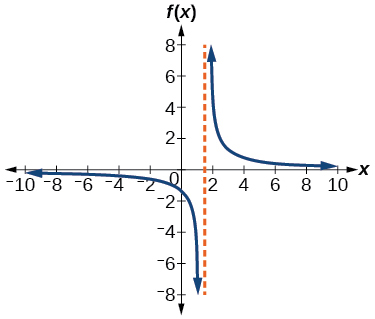
For the following exercises, identify the removable discontinuity.
For the following exercises, express a rational function that describes the situation.
A large mixing tank currently contains 200 gallons of water, into which 10 pounds of sugar have been mixed. A tap will open, pouring 10 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 3 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after minutes.
A large mixing tank currently contains 300 gallons of water, into which 8 pounds of sugar have been mixed. A tap will open, pouring 20 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 2 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after minutes.
For the following exercises, use the given rational function to answer the question.
The concentration of a drug in a patient’s bloodstream hours after injection in given by What happens to the concentration of the drug as increases?
The concentration of a drug in a patient’s bloodstream hours after injection is given by Use a calculator to approximate the time when the concentration is highest.
After about 6.12 hours.
For the following exercises, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.
An open box with a square base is to have a volume of 108 cubic inches. Find the dimensions of the box that will have minimum surface area. Let = length of the side of the base.
A rectangular box with a square base is to have a volume of 20 cubic feet. The material for the base costs 30 cents/ square foot. The material for the sides costs 10 cents/square foot. The material for the top costs 20 cents/square foot. Determine the dimensions that will yield minimum cost. Let = length of the side of the base.
2 by 2 by 5 feet.
A right circular cylinder has volume of 100 cubic inches. Find the radius and height that will yield minimum surface area. Let = radius.
A right circular cylinder with no top has a volume of 50 cubic meters. Find the radius that will yield minimum surface area. Let = radius.
Radius = 2.52 meters.
A right circular cylinder is to have a volume of 40 cubic inches. It costs 4 cents/square inch to construct the top and bottom and 1 cent/square inch to construct the rest of the cylinder. Find the radius to yield minimum cost. Let = radius.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?