| << Chapter < Page | Chapter >> Page > |
We can also approximate the value of a definite integral by using trapezoids rather than rectangles. In [link] , the area beneath the curve is approximated by trapezoids rather than by rectangles.
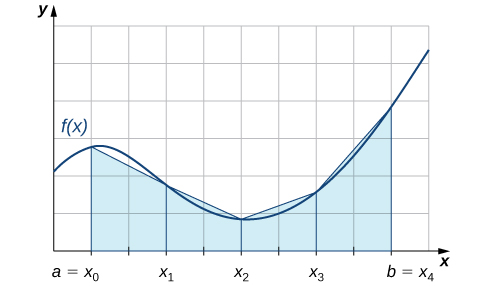
The trapezoidal rule for estimating definite integrals uses trapezoids rather than rectangles to approximate the area under a curve. To gain insight into the final form of the rule, consider the trapezoids shown in [link] . We assume that the length of each subinterval is given by First, recall that the area of a trapezoid with a height of h and bases of length and is given by We see that the first trapezoid has a height and parallel bases of length and Thus, the area of the first trapezoid in [link] is
The areas of the remaining three trapezoids are
Consequently,
After taking out a common factor of and combining like terms, we have
Generalizing, we formally state the following rule.
Assume that is continuous over Let n be a positive integer and Let be divided into subintervals, each of length with endpoints at Set
Then,
Before continuing, let’s make a few observations about the trapezoidal rule. First of all, it is useful to note that
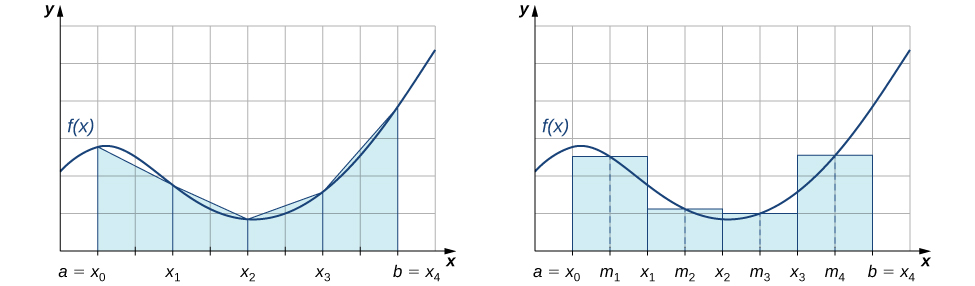
That is, and approximate the integral using the left-hand and right-hand endpoints of each subinterval, respectively. In addition, a careful examination of [link] leads us to make the following observations about using the trapezoidal rules and midpoint rules to estimate the definite integral of a nonnegative function. The trapezoidal rule tends to overestimate the value of a definite integral systematically over intervals where the function is concave up and to underestimate the value of a definite integral systematically over intervals where the function is concave down. On the other hand, the midpoint rule tends to average out these errors somewhat by partially overestimating and partially underestimating the value of the definite integral over these same types of intervals. This leads us to hypothesize that, in general, the midpoint rule tends to be more accurate than the trapezoidal rule.
Use the trapezoidal rule to estimate using four subintervals.
The endpoints of the subintervals consist of elements of the set and Thus,
An important aspect of using these numerical approximation rules consists of calculating the error in using them for estimating the value of a definite integral. We first need to define absolute error and relative error .

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?