| << Chapter < Page | Chapter >> Page > |
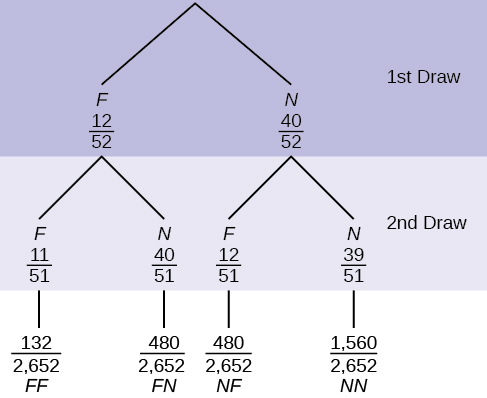
In a standard deck, there are 52 cards. Twelve cards are face cards ( F ) and 40 cards are not face cards ( N ). Draw two cards, one at a time, without replacement. The tree diagram is labeled with all possible probabilities.
A litter of kittens available for adoption at the Humane Society has four tabby kittens and five black kittens. A family comes in and randomly selects two kittens (without replacement) for adoption.
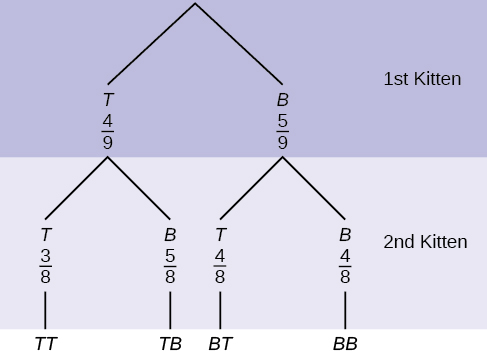
a. c, b. d, c. , d.
Suppose there are four red balls and three yellow balls in a box. Three balls are drawn from the box without replacement. What is the probability that one ball of each coloring is selected?
+
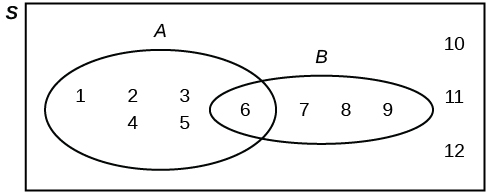
A Venn diagram is a picture that represents the outcomes of an experiment. It generally consists of a box that represents the sample space S together with circles or ovals. The circles or ovals represent events.
Suppose an experiment has the outcomes 1, 2, 3, ... , 12 where each outcome has an equal chance of occurring. Let event A = {1, 2, 3, 4, 5, 6} and event B = {6, 7, 8, 9}. Then A AND B = {6} and A OR B = {1, 2, 3, 4, 5, 6, 7, 8, 9}. The Venn diagram is as follows:
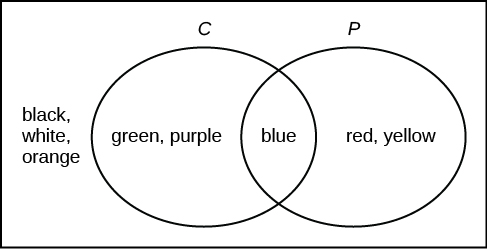
Suppose an experiment has outcomes black, white, red, orange, yellow, green, blue, and purple, where each outcome has an equal chance of occurring. Let event C = {green, blue, purple} and event P = {red, yellow, blue}. Then C AND P = {blue} and C OR P = {green, blue, purple, red, yellow}. Draw a Venn diagram representing this situation.
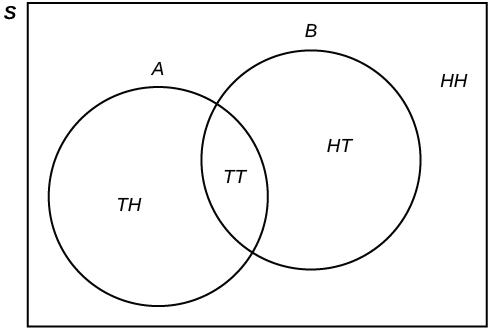
Flip two fair coins. Let A = tails on the first coin. Let B = tails on the second coin. Then A = { TT , TH } and B = { TT , HT }. Therefore, A AND B = { TT }. A OR B = { TH , TT , HT }.
The sample space when you flip two fair coins is X = { HH , HT , TH , TT }. The outcome HH is in NEITHER A NOR B . The Venn diagram is as follows:
Roll a fair, six-sided die. Let A = a prime number of dots is rolled. Let B = an odd number of dots is rolled. Then A = {2, 3, 5} and B = {1, 3, 5}. Therefore, A AND B = {3, 5}. A OR B = {1, 2, 3, 5}. The sample space for rolling a fair die is S = {1, 2, 3, 4, 5, 6}. Draw a Venn diagram representing this situation.

Forty percent of the students at a local college belong to a club and 50% work part time. Five percent of the students work part time and belong to a club. Draw a Venn diagram showing the relationships. Let C = student belongs to a club and PT = student works part time.
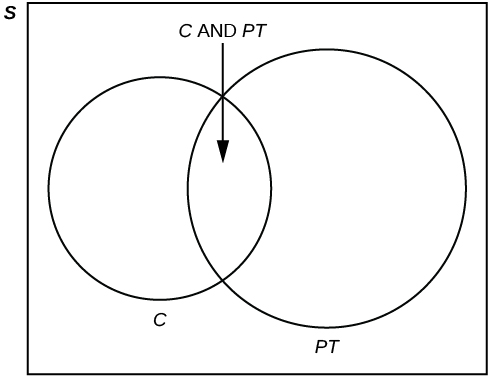
If a student is selected at random, find

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?