| << Chapter < Page | Chapter >> Page > |
In order to design an effective analysis tool, we have to be familiar with the effects of all the parameters we make available (processing gain, sequence length, SNR of channel, number of users, degree of generator polynomial). We tested our model and concluded our results were consistent with what we would expect from a CDMA system. The following are some relationships between some parameters and the bit rate error we found especially interesting.
Generator polynomial vs number of users: For an polynomial of order x, the number of users must be less than 2x in order to minimize bit error ratio. For any number of users N, the minimum order polynomial that corresponds to the number of users>N must be used in order to minimize error.
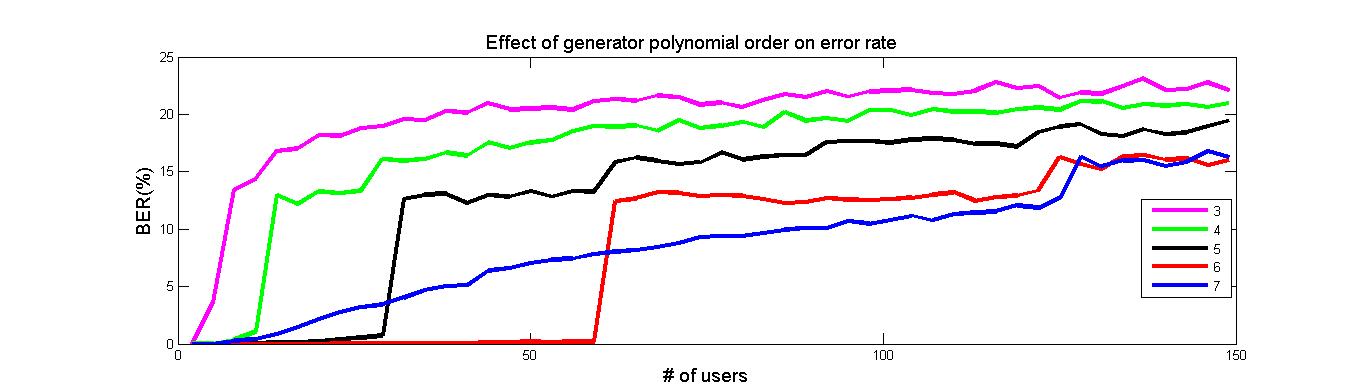
Number of users vs number of errors: As the number of users in a system increases, the bit error rate increases as well. Modulation sequences are assigned to each user by taking one PN sequence with a long period and assigning users delayed versions of the sequence. Increasing users will cause each user's sequence to be less orthogonal with the rest of the users, resulting in more errors at the receiving end.
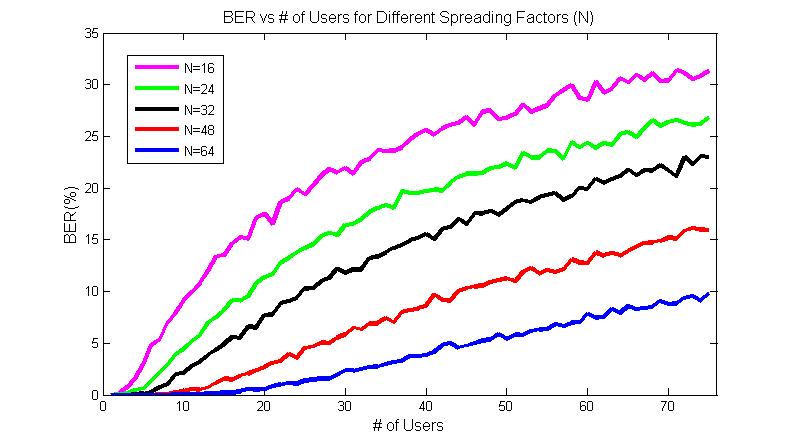
Processing Gain vs number of errors: The processor gain (also referred to as spreading factor) is the ratio of the bandwidth of the pseudo-random code to the bandwidth of our desired signal. The processing gain is also the number of "chips" used to transmit a single simple. A greater the processing gain results in fewer errors in our received signal. However, in practical applications, processing gain is limited by the available bandwidth. We plotted the effect of different processing gains against the bit error rate to observe the trade off between error rate and processing gain. This plot is shown below:
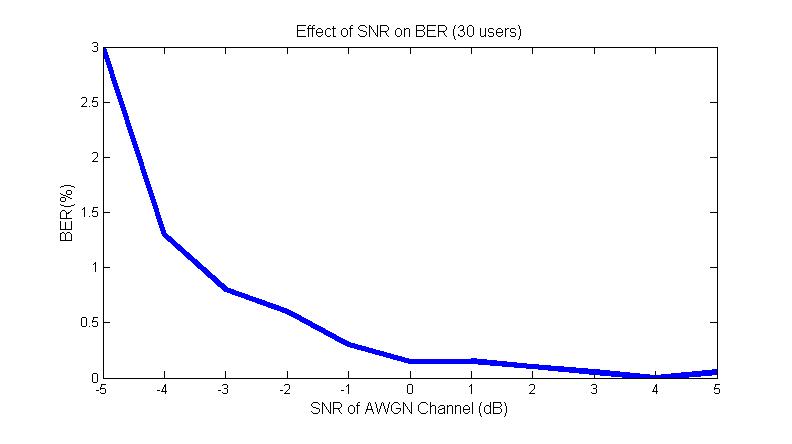
SNR vs number of users: In our model, SNR specifies the ratio of signal power to noise power in the additive white Gaussian noise channel. In a communication channel, we would like to have a high SNR. For the majority of our simulation, we set the SNR to 0(dB) to simulate a worst case scenario, where the power of the signal and the power of noise are equal. However, for a better understanding, we will show some of the effects of the SNR on few and multiple users.
First, we wanted to how SNR affected the bit error rate if the system had a small number of users (<40). Choosing 30 users for our simulation, we saw that SNR had a significant effect on bit error rate. As the SNR increases (e.x. from -5 to 5) we can see a close to quadratic relationship between the SNR and the number of errors.
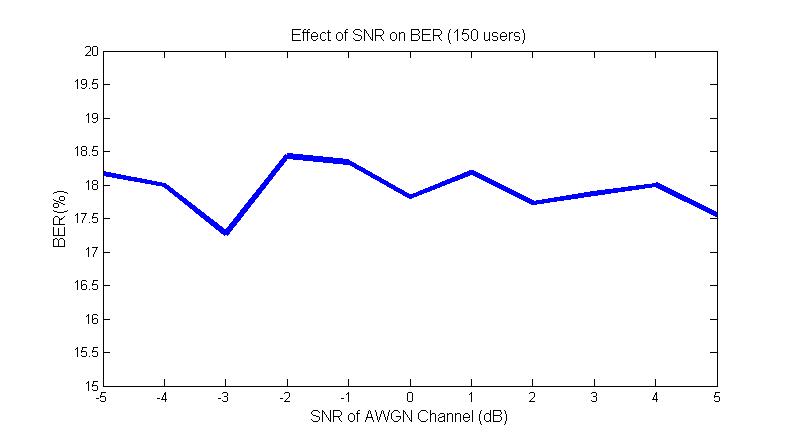
We chose to include 150 users in our system to demonstrate how SNR affected bit error rate for a large number of uers. We observe that the SNR seems to have no effect on the bit error rate. Overall, the bit error rate is high for all SNR values. When there are many users, the SNR of the channel becomes less important because the waveforms transmitted by other users look like noise. Even with a high SNR, the channel will appear noisy because of the other users. Due to the randomness of the channel the BER varies by +/- 0.5%

Notification Switch
Would you like to follow the 'Elec 301 projects fall 2011' conversation and receive update notifications?