| << Chapter < Page | Chapter >> Page > |
The great astronomer Edwin Hubble discovered that all distant galaxies are receding from our Milky Way Galaxy with velocities proportional to their distances. It appears to an observer on the Earth that we are at the center of an expanding universe. [link] illustrates this for five galaxies lying along a straight line, with the Milky Way Galaxy at the center. Using the data from the figure, calculate the velocities: (a) relative to galaxy 2 and (b) relative to galaxy 5. The results mean that observers on all galaxies will see themselves at the center of the expanding universe, and they would likely be aware of relative velocities, concluding that it is not possible to locate the center of expansion with the given information.
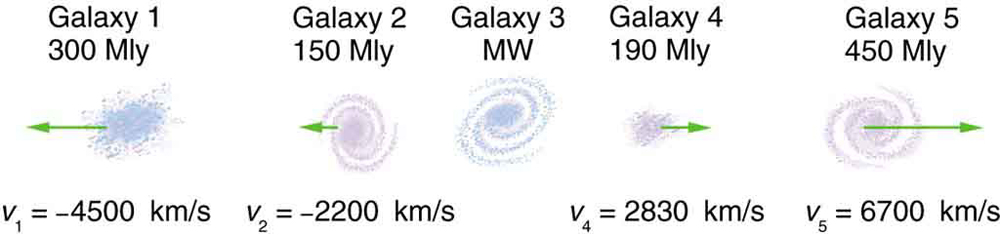
(a) Use the distance and velocity data in [link] to find the rate of expansion as a function of distance.
(b) If you extrapolate back in time, how long ago would all of the galaxies have been at approximately the same position? The two parts of this problem give you some idea of how the Hubble constant for universal expansion and the time back to the Big Bang are determined, respectively.
(a)
(b) 20.2 billion years
An athlete crosses a 25-m-wide river by swimming perpendicular to the water current at a speed of 0.5 m/s relative to the water. He reaches the opposite side at a distance 40 m downstream from his starting point. How fast is the water in the river flowing with respect to the ground? What is the speed of the swimmer with respect to a friend at rest on the ground?
A ship sailing in the Gulf Stream is heading west of north at a speed of 4.00 m/s relative to the water. Its velocity relative to the Earth is west of north. What is the velocity of the Gulf Stream? (The velocity obtained is typical for the Gulf Stream a few hundred kilometers off the east coast of the United States.)
, north of east
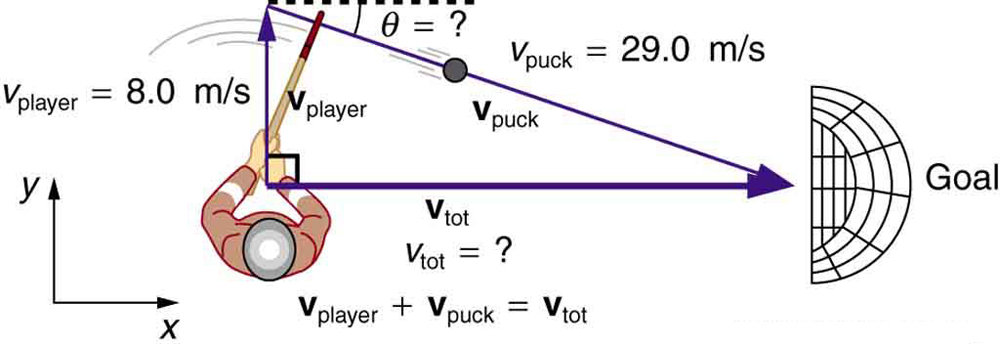
An ice hockey player is moving at 8.00 m/s when he hits the puck toward the goal. The speed of the puck relative to the player is 29.0 m/s. The line between the center of the goal and the player makes a angle relative to his path as shown in [link] . What angle must the puck’s velocity make relative to the player (in his frame of reference) to hit the center of the goal?
Unreasonable Results Suppose you wish to shoot supplies straight up to astronauts in an orbit 36,000 km above the surface of the Earth. (a) At what velocity must the supplies be launched? (b) What is unreasonable about this velocity? (c) Is there a problem with the relative velocity between the supplies and the astronauts when the supplies reach their maximum height? (d) Is the premise unreasonable or is the available equation inapplicable? Explain your answer.
Unreasonable Results A commercial airplane has an air speed of due east and flies with a strong tailwind. It travels 3000 km in a direction south of east in 1.50 h. (a) What was the velocity of the plane relative to the ground? (b) Calculate the magnitude and direction of the tailwind’s velocity. (c) What is unreasonable about both of these velocities? (d) Which premise is unreasonable?
Construct Your Own Problem Consider an airplane headed for a runway in a cross wind. Construct a problem in which you calculate the angle the airplane must fly relative to the air mass in order to have a velocity parallel to the runway. Among the things to consider are the direction of the runway, the wind speed and direction (its velocity) and the speed of the plane relative to the air mass. Also calculate the speed of the airplane relative to the ground. Discuss any last minute maneuvers the pilot might have to perform in order for the plane to land with its wheels pointing straight down the runway.

Notification Switch
Would you like to follow the 'Selected chapters of college physics for secondary 5' conversation and receive update notifications?