3.3 Trigonometric substitution  (Page 2/5)

The following example demonstrates the application of this problem-solving strategy.

Integrating an expression involving $\sqrt{a^2-x^2}$

Evaluate ${{\displaystyle \int }}^{\text{}}\sqrt{9-x^2}dx.$

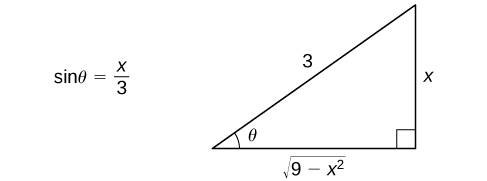
Begin by making the substitutions $x=3\text{sin}\theta$ and $dx=3\text{cos}\theta d\theta .$ Since $\text{sin}\theta =\frac{x}{3},$ we can construct the reference triangle shown in the following figure.

Thus,

$\begin{array}{ccccc}\hfill {{\displaystyle \int }}^{\text{}}\sqrt{9-x^2}dx& ={{\displaystyle \int }}^{\text{}}\sqrt{9-{(3\text{sin}\theta )}^2}3\text{cos}\theta d\theta \hfill & & & \text{Substitute}x=3\text{sin}\theta \text{and}dx=3\text{cos}\theta d\theta .\hfill \\ & ={{\displaystyle \int }}^{\text{}}\sqrt{9(1-{\text{sin}}^2\theta )}3\text{cos}\theta d\theta \hfill & & & \text{Simplify.}\hfill \\ & ={{\displaystyle \int }}^{\text{}}\sqrt{9{\text{cos}}^2\theta }3\text{cos}\theta d\theta \hfill & & & \text{Substitute}{\text{cos}}^2\theta =1-{\text{sin}}^2\theta .\hfill \\ & ={{\displaystyle \int }}^{\text{}}3\left|\text{cos}\theta \right|3\text{cos}\theta d\theta \hfill & & & \text{Take the square root.}\hfill \\ & ={{\displaystyle \int }}^{\text{}}9{\text{cos}}^2\theta d\theta \hfill & & & \begin{array}{c}\text{Simplify. Since}-\frac{\pi }{2}\le \theta \le \frac{\pi }{2},\text{cos}\theta \ge 0\text{and}\hfill \\ \left|\text{cos}\theta \right|=\text{cos}\theta .\hfill \end{array}\hfill \\ & ={{\displaystyle \int }}^{\text{}}9\left(\frac{1}{2}+\frac{1}{2}\text{cos}(2\theta )\right)d\theta \hfill & & & \begin{array}{c}\text{Use the strategy for integrating an even power}\hfill \\ \text{of}\text{cos}\theta .\hfill \end{array}\hfill \\ & =\frac{9}{2}\theta +\frac{9}{4}\text{sin}(2\theta )+C\hfill & & & \text{Evaluate the integral.}\hfill \\ & =\frac{9}{2}\theta +\frac{9}{4}(2\text{sin}\theta \text{cos}\theta )+C\hfill & & & \text{Substitute}\text{sin}(2\theta )=2\text{sin}\theta \text{cos}\theta .\hfill \\ & =\frac{9}{2}{\text{sin}}^{\mathrm{-1}}\left(\frac{x}{3}\right)+\frac{9}{2}·\frac{x}{3}·\frac{\sqrt{9-x^2}}{3}+C\hfill & & & \begin{array}{c}\text{Substitute}{\text{sin}}^{\mathrm{-1}}\left(\frac{x}{3}\right)=\theta \text{and}\text{sin}\theta =\frac{x}{3}.\text{Use}\hfill \\ \text{the reference triangle to see that}\hfill \\ \text{cos}\theta =\frac{\sqrt{9-x^2}}{3}\text{and make this substitution.}\hfill \end{array}\hfill \\ & =\frac{9}{2}{\text{sin}}^{\mathrm{-1}}\left(\frac{x}{3}\right)+\frac{x\sqrt{9-x^2}}{2}+C.\hfill & & & \text{Simplify.}\hfill \end{array}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Integrating an expression involving $\sqrt{a^2-x^2}$

Evaluate ${\displaystyle \int \frac{\sqrt{4-x^2}}{x}dx.}$

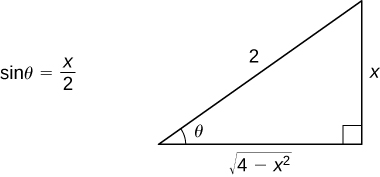
First make the substitutions $x=2\text{sin}\theta$ and $dx=2\text{cos}\theta d\theta .$ Since $\text{sin}\theta =\frac{x}{2},$ we can construct the reference triangle shown in the following figure.

Thus,

$\begin{array}{ccccc}\hfill {\displaystyle \int \frac{\sqrt{4-x^2}}{x}dx}& ={\displaystyle \int \frac{\sqrt{4-{(2\text{sin}\theta )}^2}}{2\text{sin}\theta }2\text{cos}\theta d\theta }\hfill & & & \text{Substitute}x=2\text{sin}\theta \text{and}=2\text{cos}\theta d\theta .\hfill \\ & ={\displaystyle \int \frac{2{\text{cos}}^2\theta }{\text{sin}\theta }d\theta }\hfill & & & \text{Substitute}{\text{cos}}^2\theta =1-{\text{sin}}^2\theta \text{and simplify.}\hfill \\ & ={\displaystyle \int \frac{2(1-{\text{sin}}^2\theta )}{\text{sin}\theta }d\theta }\hfill & & & \text{Substitute}{\text{sin}}^2\theta =1-{\text{cos}}^2\theta .\hfill \\ & ={{\displaystyle \int }}^{\text{}}(2\text{csc}\theta -2\text{sin}\theta )d\theta \hfill & & & \begin{array}{c}\text{Separate the numerator, simplify, and use}\hfill \\ \text{csc}\theta =\frac{1}{\text{sin}\theta }.\hfill \end{array}\hfill \\ & =2\text{ln}\left|\text{csc}\theta -\text{cot}\theta \right|+2\text{cos}\theta +C\hfill & & & \text{Evaluate the integral.}\hfill \\ & =2\text{ln}\left|\frac{2}{x}-\frac{\sqrt{4-x^2}}{x}\right|+\sqrt{4-x^2}+C.\hfill & & & \begin{array}{c}\text{Use the reference triangle to rewrite the}\hfill \\ \text{expression in terms of}x\text{and simplify.}\hfill \end{array}\hfill \end{array}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

In the next example, we see that we sometimes have a choice of methods.

Integrating expressions involving $\sqrt{a^2+x^2}$

For integrals containing $\sqrt{a^2+x^2,}$ let’s first consider the domain of this expression. Since $\sqrt{a^2+x^2}$ is defined for all real values of $x,$ we restrict our choice to those trigonometric functions that have a range of all real numbers. Thus, our choice is restricted to selecting either $x=a\text{tan}\theta$ or $x=a\text{cot}\theta .$ Either of these substitutions would actually work, but the standard substitution is $x=a\text{tan}\theta$ or, equivalently, $\text{tan}\theta =x\text{/}a.$ With this substitution, we make the assumption that $\text{−}(\pi \text{/}2)<\theta <\pi \text{/}2,$ so that we also have $\theta ={\text{tan}}^{\mathrm{-1}}\left(x\text{/}a\right).$ The procedure for using this substitution is outlined in the following problem-solving strategy.