3.3 The functions e^x and e^jθ: the euler and de moivre identities

The Euler and De Moivre identities are the fundamental identities for deriving trigonometric formulas. From the identity $e^{j\theta }=cos\theta +j$ $sin\theta$ and the conjugate identity $e^{-j\theta }={\left(e^{j\theta }\right)}^{*}=cos\theta -j$ $sin\theta$ , we have the Euler identities for $cos\theta$ and $sin\theta$ :

These identities are illustrated in [link] .

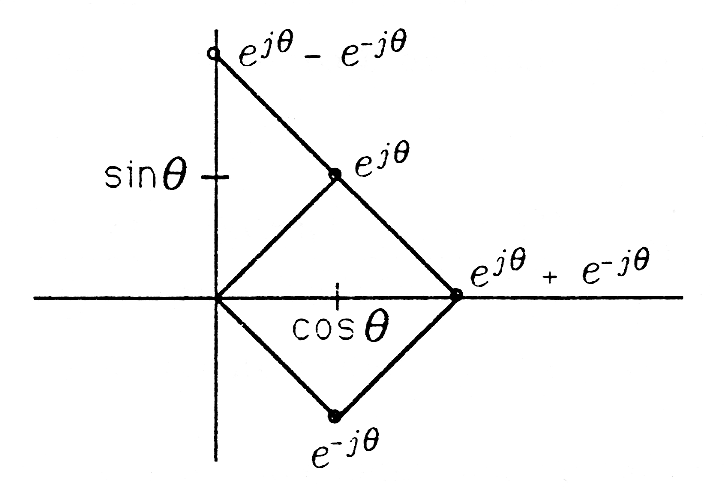
The identity $e^{j\theta }=cos\theta +jsin\theta$ also produces the De Moivre identity:

When the left-hand side of this equation is expanded with the binomial expansion, we obtain the identity

Binomial Coefficients and Pascal's Triangle. The binomial coefficients ${(}_k^n)$ in [link] are shorthand for the number

This number gives the coefficient of $x^{n-k}{y}^k$ in the expansion of ${(x+y)}^n$ . How do we know that there are ${(}_k^n)$ terms of the form $x^{n-k}{y}^k$ ? One way to answer this question is to use Pascal's triangle, illustrated in [link] . Each node on Pascal's triangle shows the number of routes that terminate at that node. This number is always the sum of the number of routes that terminate at the nodes just above the node in question. If we think of a left-hand path as an occurrence of an $x$ and a right-hand path as an occurrence of a $y$ , then we see that Pascal's triangle keeps track of the number of occurrences of $x^{n-k}{y}^k$ .