| << Chapter < Page | Chapter >> Page > |
This equation yields two solutions: and . (It is left as an exercise for the reader to verify these solutions.) The time is or . The negative value of time implies an event before the start of motion, and so we discard it. Thus,
Discussion for (a)
The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 m/s and lands 20.0 m below its starting altitude will spend 3.96 s in the air.
Solution for (b)
From the information now in hand, we can find the final horizontal and vertical velocities and and combine them to find the total velocity and the angle it makes with the horizontal. Of course, is constant so we can solve for it at any horizontal location. In this case, we chose the starting point since we know both the initial velocity and initial angle. Therefore:
The final vertical velocity is given by the following equation:
where was found in part (a) to be . Thus,
so that
To find the magnitude of the final velocity we combine its perpendicular components, using the following equation:
which gives
The direction is found from the equation:
so that
Thus,
Discussion for (b)
The negative angle means that the velocity is below the horizontal. This result is consistent with the fact that the final vertical velocity is negative and hence downward—as you would expect because the final altitude is 20.0 m lower than the initial altitude. (See [link] .)
One of the most important things illustrated by projectile motion is that vertical and horizontal motions are independent of each other. Galileo was the first person to fully comprehend this characteristic. He used it to predict the range of a projectile. On level ground, we define range to be the horizontal distance traveled by a projectile. Galileo and many others were interested in the range of projectiles primarily for military purposes—such as aiming cannons. However, investigating the range of projectiles can shed light on other interesting phenomena, such as the orbits of satellites around the Earth. Let us consider projectile range further.
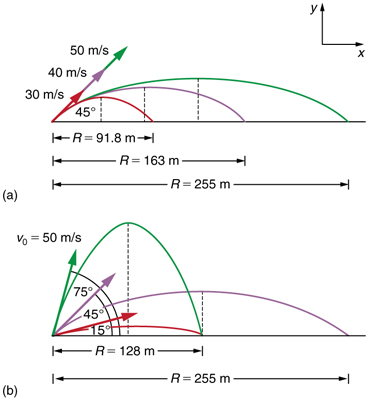
How does the initial velocity of a projectile affect its range? Obviously, the greater the initial speed , the greater the range, as shown in [link] (a). The initial angle also has a dramatic effect on the range, as illustrated in [link] (b). For a fixed initial speed, such as might be produced by a cannon, the maximum range is obtained with . This is true only for conditions neglecting air resistance. If air resistance is considered, the maximum angle is approximately . Interestingly, for every initial angle except , there are two angles that give the same range—the sum of those angles is . The range also depends on the value of the acceleration of gravity . The lunar astronaut Alan Shepherd was able to drive a golf ball a great distance on the Moon because gravity is weaker there. The range of a projectile on level ground for which air resistance is negligible is given by

Notification Switch
Would you like to follow the 'Cc test coll' conversation and receive update notifications?