| << Chapter < Page | Chapter >> Page > |
Find the arc-length parameterization for each of the following curves:
Find the arc-length function for the helix
Then, use the relationship between the arc length and the parameter t to find an arc-length parameterization of
or Substituting this into gives
An important topic related to arc length is curvature. The concept of curvature provides a way to measure how sharply a smooth curve turns. A circle has constant curvature. The smaller the radius of the circle, the greater the curvature.
Think of driving down a road. Suppose the road lies on an arc of a large circle. In this case you would barely have to turn the wheel to stay on the road. Now suppose the radius is smaller. In this case you would need to turn more sharply to stay on the road. In the case of a curve other than a circle, it is often useful first to inscribe a circle to the curve at a given point so that it is tangent to the curve at that point and “hugs” the curve as closely as possible in a neighborhood of the point ( [link] ). The curvature of the graph at that point is then defined to be the same as the curvature of the inscribed circle.
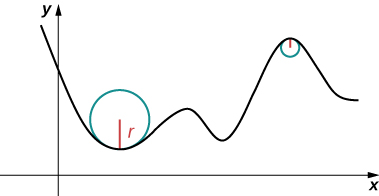
Let C be a smooth curve in the plane or in space given by where is the arc-length parameter. The curvature at s is
Visit this website for more information about the curvature of a space curve.
The formula in the definition of curvature is very useful in terms of calculation. In particular, recall that represents the unit tangent vector to a given vector-valued function and the formula for is To use the formula for curvature, it is first necessary to express in terms of the arc-length parameter s , then find the unit tangent vector for the function then take the derivative of with respect to s. This is a tedious process. Fortunately, there are equivalent formulas for curvature.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?