| << Chapter < Page | Chapter >> Page > |
(a) A 22.0 kg child is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she exert to stay on if she is 1.25 m from its center?
(b) What centripetal force does she need to stay on an amusement park merry-go-round that rotates at 3.00 rev/min if she is 8.00 m from its center?
(c) Compare each force with her weight.
a) 483 N
b) 17.4 N
c) 2.24 times her weight, 0.0807 times her weight
Calculate the centripetal force on the end of a 100 m (radius) wind turbine blade that is rotating at 0.5 rev/s. Assume the mass is 4 kg.
What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
What is the ideal speed to take a 100 m radius curve banked at a 20.0° angle?
(a) What is the radius of a bobsled turn banked at 75.0° and taken at 30.0 m/s, assuming it is ideally banked?
(b) Calculate the centripetal acceleration.
(c) Does this acceleration seem large to you?
a) 24.6 m
b)
c) This does not seem too large, but it is clear that bobsledders feel a lot of force on them going through sharply banked turns.
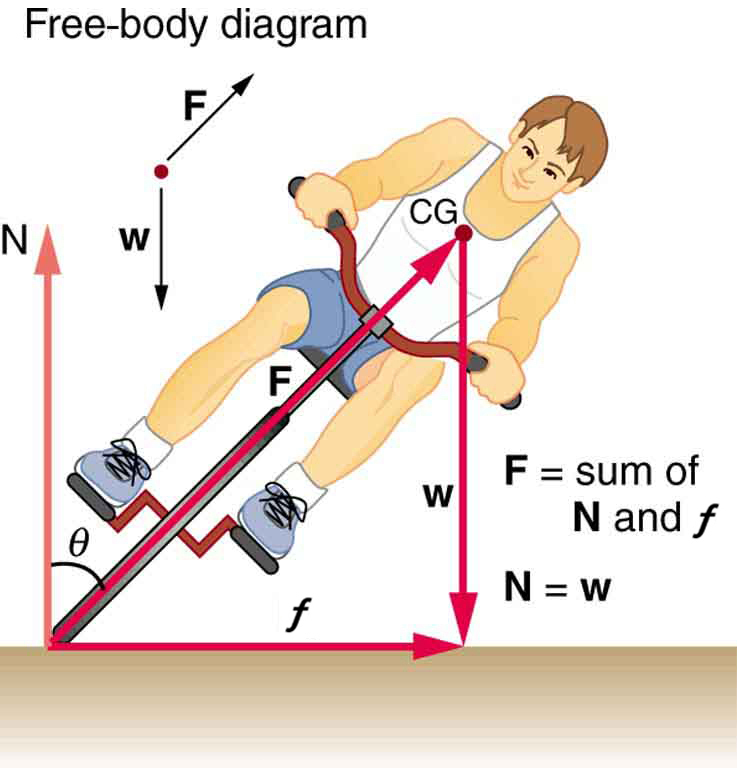
Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in [link] . To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components—friction parallel to the road (this must supply the centripetal force), and the vertical normal force (which must equal the system’s weight).
(a) Show that (as defined in the figure) is related to the speed and radius of curvature of the turn in the same way as for an ideally banked roadway—that is,
(b) Calculate for a 12.0 m/s turn of radius 30.0 m (as in a race).
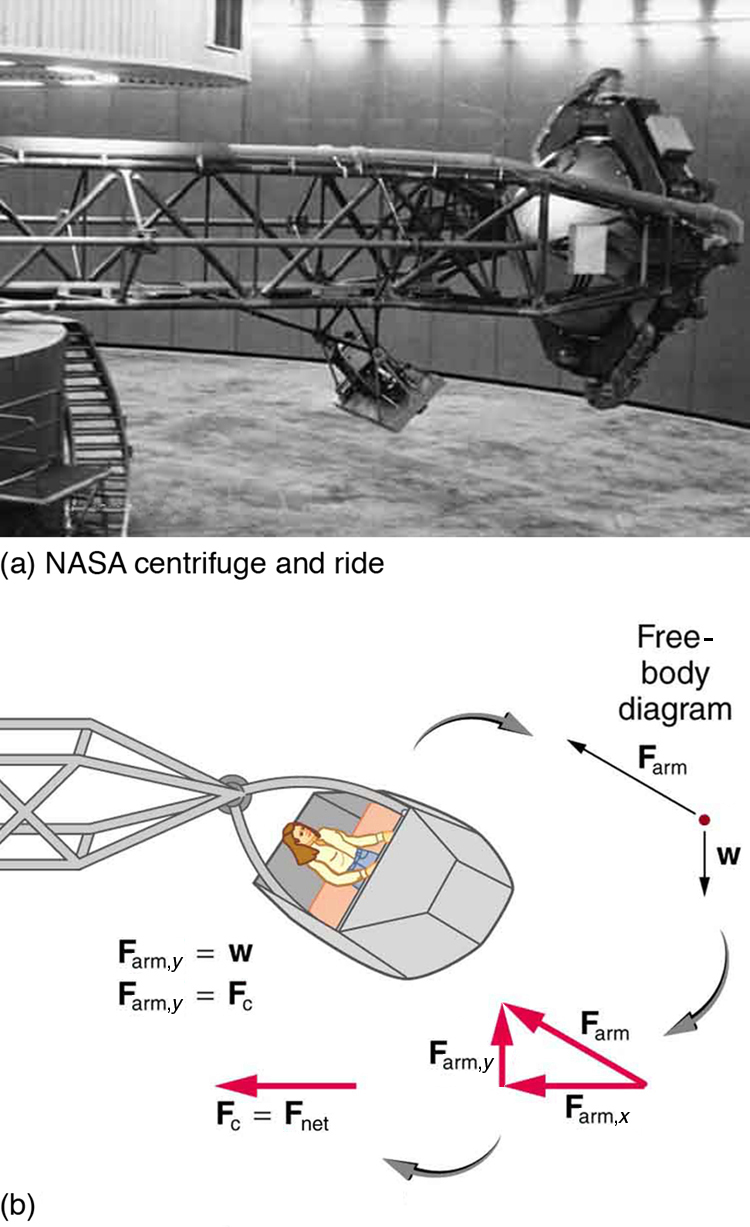
A large centrifuge, like the one shown in [link] (a), is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric reentries.
(a) At what angular velocity is the centripetal acceleration if the rider is 15.0 m from the center of rotation?
(b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in [link] (b). At what angle below the horizontal will the cage hang when the centripetal acceleration is ? (Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free body diagram of the forces to see what the angle should be.)
a) 2.56 rad/s
b)
Integrated Concepts
If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads). (a) Calculate the ideal speed to take a 100 m radius curve banked at 15.0º. (b) What is the minimum coefficient of friction needed for a frightened driver to take the same curve at 20.0 km/h?
a) 16.2 m/s
b) 0.234
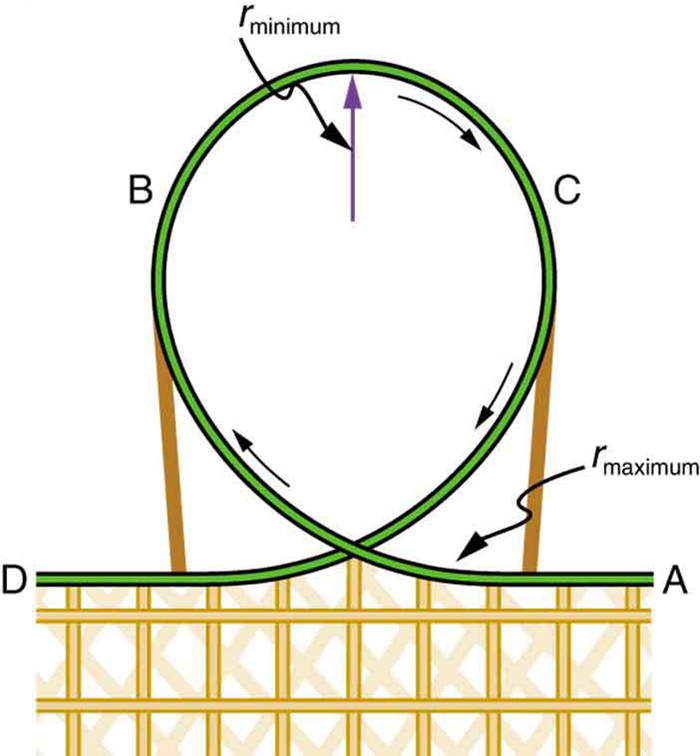
Modern roller coasters have vertical loops like the one shown in [link] . The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?
Unreasonable Results
(a) Calculate the minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s.
(b) What is unreasonable about the result?
(c) Which premises are unreasonable or inconsistent?
a) 1.84
b) A coefficient of friction this much greater than 1 is unreasonable .
c) The assumed speed is too great for the tight curve.

Notification Switch
Would you like to follow the 'Physics subject knowledge enhancement course (ske)' conversation and receive update notifications?