| << Chapter < Page | Chapter >> Page > |
Working rules : We shall be using following definitions/results for solving problems in this module :
Problem : Find the domain of the function given by (Be aware that "x" appears as base of given logrithmic function):
Solution : By definition of logarithmic function, we know that base of logarithmic function is a positive number excluding x =1.
Hence, domain of the given function is :
Domain of the function

or,
Problem : Find the domain of the function given by :
Solution : The argument (input to the function) of logarithmic function is a rational function. We need to find values of “x” such that the argument of the function evaluates to a positive number. Hence,
In this case, we can not apply sign scheme for the rational function as a whole. Reason is that the quadratic equation in the denominator has no real roots and as such can not be factorized in linear factors. We see that discreminant,"D", of the quadratic equation in the denominator, is negative :
The quadratic expression in denominator is positive for all value of x as coefficient of squared term is positive. Clearly, sign of rational function is same as that of quadratic expression in the numerator. The coefficient of squared term of the numerator “ ”, is positive for all values of “x”. The quadratic expression in the numerator evaluates to positive for intervals beyond root values. The roots of the corresponding equal equation is :
Domain of the function
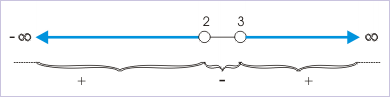
Problem : Find the domain of the function given by :
Solution : The function is a square root of a logarithmic function. On the other hand argument of logarithmic function is a rational function. In order to find the domain of the given function, we first determine what values of “x” are valid for logarithmic function. Then, we apply the condition that expression within square root should be non-negative number. Domain of given function is intersection of intervals of x obtained for each of these conditions. Now, we know that argument (input to function) of logarithmic function is a positive number. This implies that we need to find the interval of “x” for which,
In above step, we should emphasize here that we multiply “8” and “0” and retain the inequality sign because 8>0. Now, we multiply the inequality by “-1”. Therefore, inequality sign is reversed.
Here, roots of corresponding quadratic equation “ ” is x = 0, 6. It means that middle interval between “0 and 6” is negative as coefficient of “ ” is positive i.e. 6>0. Hence, interval satisfying the inequality is :
Domain of the function


Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?