| << Chapter < Page | Chapter >> Page > |
The more tightly bound a system is, the stronger the forces that hold it together and the greater the energy required to pull it apart. We can therefore learn about nuclear forces by examining how tightly bound the nuclei are. We define the binding energy (BE) of a nucleus to be the energy required to completely disassemble it into separate protons and neutrons . We can determine the BE of a nucleus from its rest mass. The two are connected through Einstein’s famous relationship . A bound system has a smaller mass than its separate constituents; the more tightly the nucleons are bound together, the smaller the mass of the nucleus.
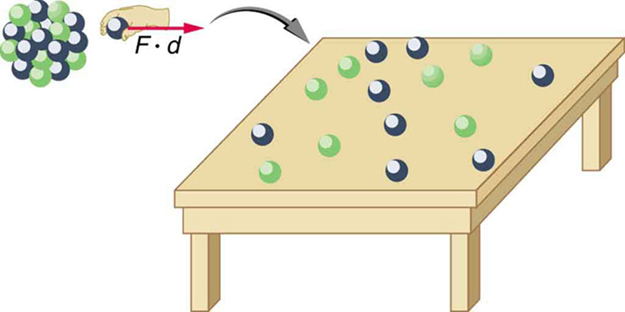
Imagine pulling a nuclide apart as illustrated in [link] . Work done to overcome the nuclear forces holding the nucleus together puts energy into the system. By definition, the energy input equals the binding energy BE. The pieces are at rest when separated, and so the energy put into them increases their total rest mass compared with what it was when they were glued together as a nucleus. That mass increase is thus . This difference in mass is known as mass defect . It implies that the mass of the nucleus is less than the sum of the masses of its constituent protons and neutrons. A nuclide has protons and neutrons, so that the difference in mass is
Thus,
where is the mass of the nuclide , is the mass of a proton, and is the mass of a neutron. Traditionally, we deal with the masses of neutral atoms. To get atomic masses into the last equation, we first add electrons to , which gives , the atomic mass of the nuclide. We then add electrons to the protons, which gives , or times the mass of a hydrogen atom. Thus the binding energy of a nuclide is
The atomic masses can be found in Appendix A , most conveniently expressed in unified atomic mass units u ( ). BE is thus calculated from known atomic masses.
Nuclear Decay Helps Explain Earth’s Hot Interior
A puzzle created by radioactive dating of rocks is resolved by radioactive heating of Earth’s interior. This intriguing story is another example of how small-scale physics can explain large-scale phenomena.
Radioactive dating plays a role in determining the approximate age of the Earth. The oldest rocks on Earth solidified about years ago—a number determined by uranium-238 dating. These rocks could only have solidified once the surface of the Earth had cooled sufficiently. The temperature of the Earth at formation can be estimated based on gravitational potential energy of the assemblage of pieces being converted to thermal energy. Using heat transfer concepts discussed in Thermodynamics it is then possible to calculate how long it would take for the surface to cool to rock-formation temperatures. The result is about years. The first rocks formed have been solid for years, so that the age of the Earth is approximately years. There is a large body of other types of evidence (both Earth-bound and solar system characteristics are used) that supports this age. The puzzle is that, given its age and initial temperature, the center of the Earth should be much cooler than it is today (see [link] ).
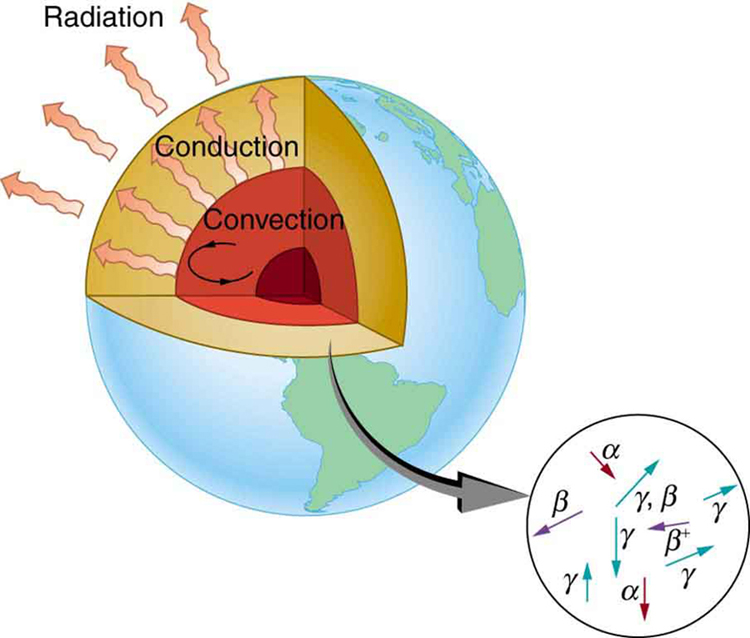
We know from seismic waves produced by earthquakes that parts of the interior of the Earth are liquid. Shear or transverse waves cannot travel through a liquid and are not transmitted through the Earth’s core. Yet compression or longitudinal waves can pass through a liquid and do go through the core. From this information, the temperature of the interior can be estimated. As noticed, the interior should have cooled more from its initial temperature in the years since its formation. In fact, it should have taken no more than about years to cool to its present temperature. What is keeping it hot? The answer seems to be radioactive decay of primordial elements that were part of the material that formed the Earth (see the blowup in [link] ).
Nuclides such as and have half-lives similar to or longer than the age of the Earth, and their decay still contributes energy to the interior. Some of the primordial radioactive nuclides have unstable decay products that also release energy— has a long decay chain of these. Further, there were more of these primordial radioactive nuclides early in the life of the Earth, and thus the activity and energy contributed were greater then (perhaps by an order of magnitude). The amount of power created by these decays per cubic meter is very small. However, since a huge volume of material lies deep below the surface, this relatively small amount of energy cannot escape quickly. The power produced near the surface has much less distance to go to escape and has a negligible effect on surface temperatures.
A final effect of this trapped radiation merits mention. Alpha decay produces helium nuclei, which form helium atoms when they are stopped and capture electrons. Most of the helium on Earth is obtained from wells and is produced in this manner. Any helium in the atmosphere will escape in geologically short times because of its high thermal velocity.

Notification Switch
Would you like to follow the 'Physics 101' conversation and receive update notifications?