2.7 Cylindrical and spherical coordinates (Page 2/11)

Calculus volume 3 Page 2 / 11

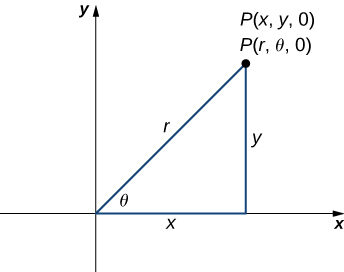
This figure is the first quadrant of the rectangular coordinate system. There is a point labeled “P = (x, y, 0) = (r, theta, 0).” There is a line segment from the origin to point P. This line segment is labeled “r.” The angle between the x-axis and the line segment r is labeled “theta.” There is also a vertical line segment labeled “y” from P to the x-axis. It forms a right triangle. — The Pythagorean theorem provides equation $r^{2} = x^{2} + y^{2} .$ Right-triangle relationships tell us that $x = r cos θ,$ $y = r sin θ,$ and $tan θ = y / x .$

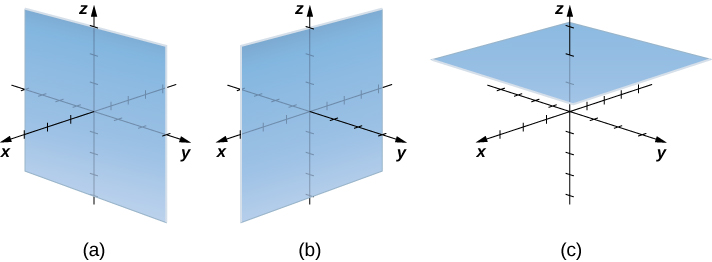
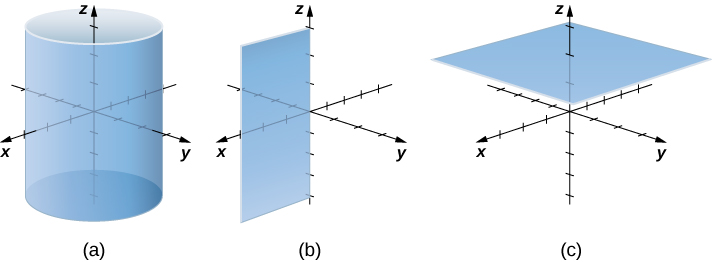
Let’s consider the differences between rectangular and cylindrical coordinates by looking at the surfaces generated when each of the coordinates is held constant. If $c$ is a constant, then in rectangular coordinates, surfaces of the form $x = c,$ $y = c,$ or $z = c$ are all planes. Planes of these forms are parallel to the yz -plane, the xz -plane, and the xy -plane, respectively. When we convert to cylindrical coordinates, the z -coordinate does not change. Therefore, in cylindrical coordinates, surfaces of the form $z = c$ are planes parallel to the xy -plane. Now, let’s think about surfaces of the form $r = c .$ The points on these surfaces are at a fixed distance from the z -axis. In other words, these surfaces are vertical circular cylinders. Last, what about $θ = c ?$ The points on a surface of the form $θ = c$ are at a fixed angle from the x -axis, which gives us a half-plane that starts at the z -axis ( [link] and [link] ).

This figure has 3 images. The first image is a plane in the 3-dimensional coordinate system. It is parallel to the y z-plane where x = c. The second image is a plane in the 3-dimensional coordinate system. It is parallel to the x z-plane where y = c. the third image is a plane in the 3-dimensional coordinate system where z = c. — In rectangular coordinates, (a) surfaces of the form $x = c$ are planes parallel to the yz -plane, (b) surfaces of the form $y = c$ are planes parallel to the xz -plane, and (c) surfaces of the form $z = c$ are planes parallel to the xy -plane.

This figure has 3 images. The first image is a right circular cylinder in the 3-dimensional coordinate system. It has the z-axis in the middle. The second image is a plane in the 3-dimensional coordinate system. It is vertical with the z-axis on one edge. The third image is a plane in the 3-dimensional coordinate system where z = c. — In cylindrical coordinates, (a) surfaces of the form $r = c$ are vertical cylinders of radius $r,$ (b) surfaces of the form $θ = c$ are half-planes at angle $θ$ from the x -axis, and (c) surfaces of the form $z = c$ are planes parallel to the xy -plane.

Converting from cylindrical to rectangular coordinates

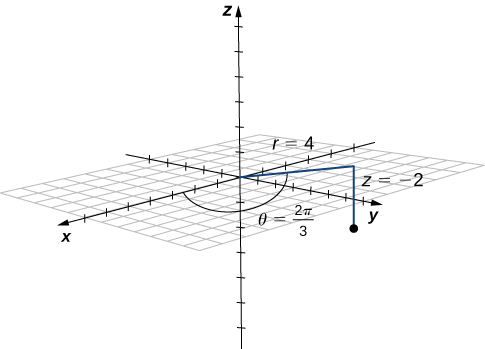
Plot the point with cylindrical coordinates $(4, \frac{2 π}{3}, −2)$ and express its location in rectangular coordinates.

Conversion from cylindrical to rectangular coordinates requires a simple application of the equations listed in [link] :

\begin{matrix} x & = & r cos θ = 4 cos \frac{2 π}{3} = −2 \\ y & = & r sin θ = 4 sin \frac{2 π}{3} = 2 \sqrt{3} \\ z & = & −2. \end{matrix}

The point with cylindrical coordinates $(4, \frac{2 π}{3}, −2)$ has rectangular coordinates $(−2, 2 \sqrt{3}, −2)$ (see the following figure).

This figure is the 3-dimensional coordinate system. It has a point where r = 4, z = -2 and theta = 2 pi /3. — The projection of the point in the xy -plane is 4 units from the origin. The line from the origin to the point’s projection forms an angle of $\frac{2 π}{3}$ with the positive x -axis. The point lies $2$ units below the xy -plane.

Got questions? Get instant answers now!

Point $R$ has cylindrical coordinates $(5, \frac{π}{6}, 4)$ . Plot $R$ and describe its location in space using rectangular, or Cartesian, coordinates.

The rectangular coordinates of the point are $(\frac{5 \sqrt{3}}{2}, \frac{5}{2}, 4) .$
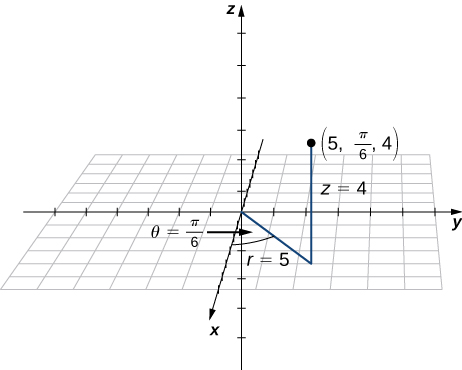
This figure is the 3-dimensional coordinate system. There is a point labeled “(5, pi/6, 4).” The point is located above a line segment in the x y-plane labeled r = 5 that is pi/6 degrees from the x-axis. The distance from the x y-plane to the point is labeled “z = 4.”

Got questions? Get instant answers now!

If this process seems familiar, it is with good reason. This is exactly the same process that we followed in Introduction to Parametric Equations and Polar Coordinates to convert from polar coordinates to two-dimensional rectangular coordinates.

Converting from rectangular to cylindrical coordinates

Convert the rectangular coordinates $(1, −3, 5)$ to cylindrical coordinates.

Use the second set of equations from [link] to translate from rectangular to cylindrical coordinates:

\begin{matrix} r^{2} & = & x^{2} + y^{2} \\ r & = & ± \sqrt{1^{2} + {(−3)}^{2}} = ± \sqrt{10} . \end{matrix}

We choose the positive square root, so $r = \sqrt{10} .$ Now, we apply the formula to find $θ .$ In this case, $y$ is negative and $x$ is positive, which means we must select the value of $θ$ between $\frac{3 π}{2}$ and $2 π :$

\begin{matrix} tan θ & = & \frac{y}{x} = \frac{−3}{1} \\ θ & = & arctan (−3) \approx 5.03 rad . \end{matrix}

In this case, the z -coordinates are the same in both rectangular and cylindrical coordinates:

z = 5 .

The point with rectangular coordinates $(1, −3, 5)$ has cylindrical coordinates approximately equal to $(\sqrt{10}, 5.03, 5) .$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	Respiratory System Drugs By CB Biern Start Quiz
	Young Economist MCQ Test By Robert Murphy Start Test
	Pre-class Online Quiz - Case Control Studies By Mucho Mizinduko Start Quiz
	Anthropology Life Cycle By Richley Crapo Start Assignment
	6 BOD Respiratory Exam By Brooke Delaney Start Exam
	2 Human A&P 2- Test 2 By Madison Christian Start Flashcards
	4 BOD Hemolymphatic -Dr. Han By Brooke Delaney Start Exam
	2 Week 2 Social Psych By Yacoub Jayoghli Start Quiz
	3 Pharmacology Excl. Nervous System MCQ By Rohini Ajay Start Quiz
	2 Gastrointestinal Pathophysiology Self-Assessment By Laurence Bailen Start Assessment