| << Chapter < Page | Chapter >> Page > |
Suppose a car merges into freeway traffic on a 200-m-long ramp. If its initial velocity is 10.0 m/s and it accelerates at , how long does it take to travel the 200 m up the ramp? (Such information might be useful to a traffic engineer.)
Strategy
Draw a sketch.
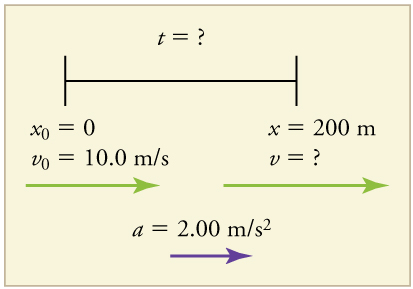
We are asked to solve for the time . As before, we identify the known quantities in order to choose a convenient physical relationship (that is, an equation with one unknown, ).
Solution
1. Identify the knowns and what we want to solve for. We know that ; ; and .
2. We need to solve for . Choose the best equation. works best because the only unknown in the equation is the variable for which we need to solve.
3. We will need to rearrange the equation to solve for . In this case, it will be easier to plug in the knowns first.
4. Simplify the equation. The units of meters (m) cancel because they are in each term. We can get the units of seconds (s) to cancel by taking , where is the magnitude of time and s is the unit. Doing so leaves
5. Use the quadratic formula to solve for .
(a) Rearrange the equation to get 0 on one side of the equation.
This is a quadratic equation of the form
where the constants are .
(b) Its solutions are given by the quadratic formula:
This yields two solutions for , which are
In this case, then, the time is in seconds, or
A negative value for time is unreasonable, since it would mean that the event happened 20 s before the motion began. We can discard that solution. Thus,
Discussion
Whenever an equation contains an unknown squared, there will be two solutions. In some problems both solutions are meaningful, but in others, such as the above, only one solution is reasonable. The 10.0 s answer seems reasonable for a typical freeway on-ramp.
With the basics of kinematics established, we can go on to many other interesting examples and applications. In the process of developing kinematics, we have also glimpsed a general approach to problem solving that produces both correct answers and insights into physical relationships. Problem-Solving Basics discusses problem-solving basics and outlines an approach that will help you succeed in this invaluable task.
We have been using SI units of meters per second squared to describe some examples of acceleration or deceleration of cars, runners, and trains. To achieve a better feel for these numbers, one can measure the braking deceleration of a car doing a slow (and safe) stop. Recall that, for average acceleration, . While traveling in a car, slowly apply the brakes as you come up to a stop sign. Have a passenger note the initial speed in miles per hour and the time taken (in seconds) to stop. From this, calculate the deceleration in miles per hour per second. Convert this to meters per second squared and compare with other decelerations mentioned in this chapter. Calculate the distance traveled in braking.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?