| << Chapter < Page | Chapter >> Page > |
Find parametric and symmetric equations for the line formed by the intersection of the planes given by and (see the following figure).
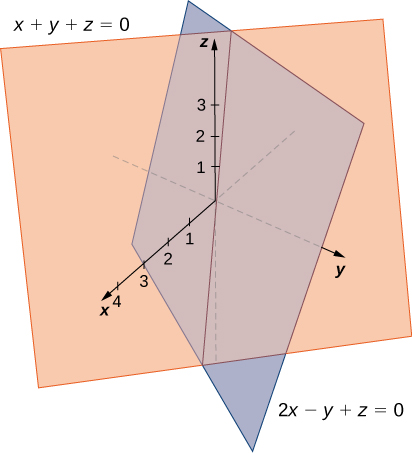
Note that the two planes have nonparallel normals, so the planes intersect. Further, the origin satisfies each equation, so we know the line of intersection passes through the origin. Add the plane equations so we can eliminate the one of the variables, in this case,
This gives us We substitute this value into the first equation to express in terms of
We now have the first two variables, and in terms of the third variable, Now we define in terms of To eliminate the need for fractions, we choose to define the parameter as Then, Substituting the parametric representation of back into the other two equations, we see that the parametric equations for the line of intersection are The symmetric equations for the line are
Find parametric equations for the line formed by the intersection of planes and
In addition to finding the equation of the line of intersection between two planes, we may need to find the angle formed by the intersection of two planes. For example, builders constructing a house need to know the angle where different sections of the roof meet to know whether the roof will look good and drain properly. We can use normal vectors to calculate the angle between the two planes. We can do this because the angle between the normal vectors is the same as the angle between the planes. [link] shows why this is true.
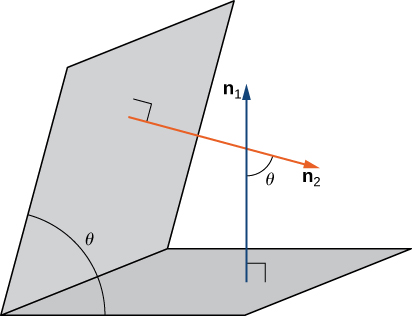
We can find the measure of the angle θ between two intersecting planes by first finding the cosine of the angle, using the following equation:
We can then use the angle to determine whether two planes are parallel or orthogonal or if they intersect at some other angle.
Determine whether each pair of planes is parallel, orthogonal, or neither. If the planes are intersecting, but not orthogonal, find the measure of the angle between them. Give the answer in radians and round to two decimal places.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?