| << Chapter < Page | Chapter >> Page > |
Describe the relationship between the lines with the following parametric equations:
These lines are skew because their direction vectors are not parallel and there is no point that lies on both lines.
We know that a line is determined by two points. In other words, for any two distinct points, there is exactly one line that passes through those points, whether in two dimensions or three. Similarly, given any three points that do not all lie on the same line, there is a unique plane that passes through these points. Just as a line is determined by two points, a plane is determined by three.
This may be the simplest way to characterize a plane, but we can use other descriptions as well. For example, given two distinct, intersecting lines, there is exactly one plane containing both lines. A plane is also determined by a line and any point that does not lie on the line. These characterizations arise naturally from the idea that a plane is determined by three points. Perhaps the most surprising characterization of a plane is actually the most useful.
Imagine a pair of orthogonal vectors that share an initial point. Visualize grabbing one of the vectors and twisting it. As you twist, the other vector spins around and sweeps out a plane. Here, we describe that concept mathematically. Let be a vector and be a point. Then the set of all points such that is orthogonal to forms a plane ( [link] ). We say that is a normal vector , or perpendicular to the plane. Remember, the dot product of orthogonal vectors is zero. This fact generates the vector equation of a plane : Rewriting this equation provides additional ways to describe the plane:
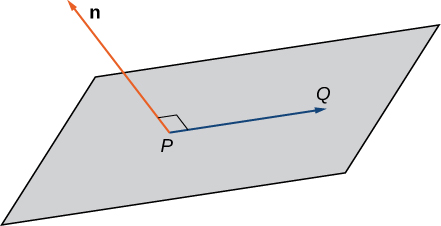
Given a point and vector the set of all points satisfying the equation forms a plane. The equation
is known as the vector equation of a plane.
The scalar equation of a plane containing point with normal vector is
This equation can be expressed as where This form of the equation is sometimes called the general form of the equation of a plane .
As described earlier in this section, any three points that do not all lie on the same line determine a plane. Given three such points, we can find an equation for the plane containing these points.
Write an equation for the plane containing points and in both standard and general forms.
To write an equation for a plane, we must find a normal vector for the plane. We start by identifying two vectors in the plane:
The cross product is orthogonal to both and so it is normal to the plane that contains these two vectors:
Thus, and we can choose any of the three given points to write an equation of the plane:

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?