2.5 Equations of lines and planes in space

By now, we are familiar with writing equations that describe a line in two dimensions. To write an equation for a line, we must know two points on the line, or we must know the direction of the line and at least one point through which the line passes. In two dimensions, we use the concept of slope to describe the orientation, or direction, of a line. In three dimensions, we describe the direction of a line using a vector parallel to the line. In this section, we examine how to use equations to describe lines and planes in space.

Equations for a line in space

Let’s first explore what it means for two vectors to be parallel. Recall that parallel vectors must have the same or opposite directions. If two nonzero vectors, $\text{u}$ and $\text{v},$ are parallel, we claim there must be a scalar, $k,$ such that $\text{u}=k\text{v}.$ If $\text{u}$ and $\text{v}$ have the same direction, simply choose $k=\frac{\Vert \text{u}\Vert }{\Vert \text{v}\Vert }.$ If $\text{u}$ and $\text{v}$ have opposite directions, choose $k=-\frac{\Vert \text{u}\Vert }{\Vert \text{v}\Vert }.$ Note that the converse holds as well. If $\text{u}=k\text{v}$ for some scalar $\text{k},$ then either $\text{u}$ and $\text{v}$ have the same direction $\left(k>0\right)$ or opposite directions $\left(k<0\right),$ so $\text{u}$ and $\text{v}$ are parallel. Therefore, two nonzero vectors $\text{u}$ and $\text{v}$ are parallel if and only if $\text{u}=k\text{v}$ for some scalar $\text{k}.$ By convention, the zero vector $0$ is considered to be parallel to all vectors.

As in two dimensions, we can describe a line in space using a point on the line and the direction of the line, or a parallel vector, which we call the direction vector    ( [link] ). Let $L$ be a line in space passing through point $P\left(x_0,y_0,z_0\right).$ Let $\text{v}=⟨a,b,c⟩$ be a vector parallel to $L.$ Then, for any point on line $Q\left(x,y,z\right),$ we know that $\overrightarrow{PQ}$ is parallel to $\text{v}.$ Thus, as we just discussed, there is a scalar, $t,$ such that $\overrightarrow{PQ}=t\text{v},$ which gives

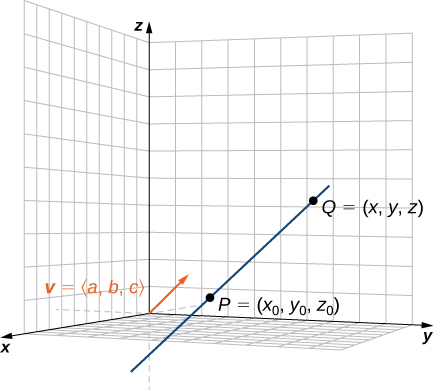
Using vector operations, we can rewrite [link] as

Setting $\text{r}=⟨x,y,z⟩$ and ${\text{r}}_0=⟨x_0,y_0,z_0⟩,$ we now have the vector equation of a line    :

Equating components, [link] shows that the following equations are simultaneously true: $x-x_0=ta,$ $y-y_0=tb,$ and $z-z_0=tc.$ If we solve each of these equations for the component variables $x,y,\text{and}z,$ we get a set of equations in which each variable is defined in terms of the parameter t and that, together, describe the line. This set of three equations forms a set of parametric equations of a line    :

If we solve each of the equations for $t$ assuming $a,b,\text{and}c$ are nonzero, we get a different description of the same line:

Because each expression equals t , they all have the same value. We can set them equal to each other to create symmetric equations of a line    :

We summarize the results in the following theorem.