| << Chapter < Page | Chapter >> Page > |
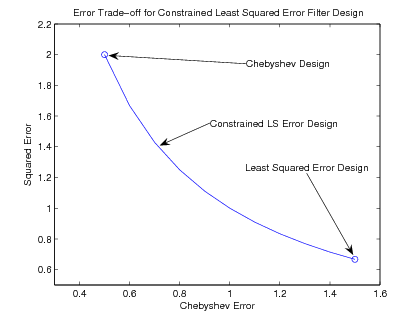
In many filter design problems, more than one criterion is important. For example, both and may be of interest in one filter. Often one is posed as a constraint and the other as an optimized variable.Indeed, because approximation minimizes the error energy and because Parseval's theorem states that an optimal frequency domain approximation is also an optimal time domain approximation, an constrained minimum error approximation seems a good practical approach. To see how this might have advantages, it isinformative to examine the relationship of the error to the error as the constraint is varied from tight to loose [link] , [link] in [link] . From this one can see just how sensitive one error is to the other and how the traditional designs are extremes on this diagram.
Another trade-off is the error in a Chebyshev design as a function of the transition band location. There are certain locations of transition bandor band edges that give much lower ripple size than others. Rabiner has examined that relation [link] , [link] .
There are problems where the peak error or Chebyshev error is important. This can be minimized directly using the Remez exchange algorithm but, inmany cases, is better controlled by use of a peak error constraint on the basic least squared error formulation of the problem [link] , [link] , [link] , [link] . An efficient algorithm for minimizing the constrained least squared error uses Lagrange multipliers [link] , [link] and the Kuhn-Tucker conditions [link] , [link] .
Similar to the Chebyshev design problem, there are two formulations of the problem: one where there is a well defined transition band separating thedesired signal spectrum (passband) from the noise or interfering signal spectrum (stopband) and the second where there is a well defined frequencythat separates the pass and stopband but no well defined transition band.
The first case would include situations with signals residing in specified bands separated by “guard bands" such as commercial radio and TVtransmissions. It also includes cases where due to multirate sampling, certain well defined bands are aliased into other well defined bands. TheParks-McClellan and Shpak-Antoniou Chebyshev designs address this case for the Chebyshev error.Adams' method [link] , [link] , [link] , [link] , [link] , [link] described below applies to the constrained least squares design with a specified transition band.
The second case would include signals with known spectral support with additive white or broad-band noise. In these cases there is no obvioustransition band or “don't care" band. The Hoffstetter-Oppenheim-Siegel and the method of the section Chebyshev Approximations using the Exchange Algorithms address this case for a Chebyshev design. The method in section below applies to the constrained least squaresdesign [link] without a specified transition band.
To pose the constrained least squared error optimization problem, we use a Lagrange multiplier formulation. First define the Lagrangian as

Notification Switch
Would you like to follow the 'Digital signal processing and digital filter design (draft)' conversation and receive update notifications?