| << Chapter < Page | Chapter >> Page > |
Find all vectors that satisfy the equation
where is any real number
Solve the equation where is a nonzero vector with a magnitude of
[T] A mechanic uses a 12-in. wrench to turn a bolt. The wrench makes a angle with the horizontal. If the mechanic applies a vertical force of lb on the wrench handle, what is the magnitude of the torque at point (see the following figure)? Express the answer in foot-pounds rounded to two decimal places.
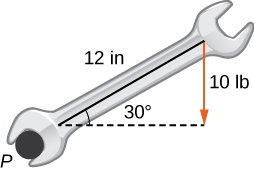
8.66 ft-lb
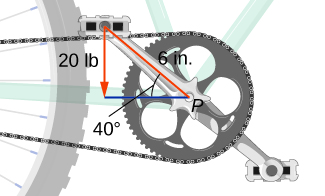
[T] A boy applies the brakes on a bicycle by applying a downward force of lb on the pedal when the 6-in. crank makes a angle with the horizontal (see the following figure). Find the torque at point Express your answer in foot-pounds rounded to two decimal places.
[T] Find the magnitude of the force that needs to be applied to the end of a 20-cm wrench located on the positive direction of the y -axis if the force is applied in the direction and it produces a N·m torque to the bolt located at the origin.
250 N
[T] What is the magnitude of the force required to be applied to the end of a 1-ft wrench at an angle of to produce a torque of N·m?
[T] The force vector acting on a proton with an electric charge of (in coulombs) moving in a magnetic field where the velocity vector is given by (here, is expressed in meters per second, is in tesla [T], and is in newtons [N]). Find the force that acts on a proton that moves in the xy -plane at velocity (in meters per second) in a magnetic field given by
[T] The force vector acting on a proton with an electric charge of moving in a magnetic field where the velocity vector v is given by (here, is expressed in meters per second, in and in If the magnitude of force acting on a proton is N and the proton is moving at the speed of 300 m/sec in magnetic field of magnitude 2.4 T, find the angle between velocity vector of the proton and magnetic field Express the answer in degrees rounded to the nearest integer.
[T] Consider the position vector of a particle at time where the components of are expressed in centimeters and time in seconds. Let be the position vector of the particle after sec.
a.
b.
A solar panel is mounted on the roof of a house. The panel may be regarded as positioned at the points of coordinates (in meters) and (see the following figure).


Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?