2.4 Arc length of a curve and surface area (Page 2/8)

Calculus volume 2 Page 2 / 8

Arc Length = lim_{n \to \infty} \sum_{i = 1}^{n} \sqrt{1 + {[f^{'} (x_{i}^{*})]}^{2}} Δ x = \int_{a}^{b} \sqrt{1 + {[f^{'} (x)]}^{2}} d x .

We summarize these findings in the following theorem.

Arc length for y = f ( x )

Let $f (x)$ be a smooth function over the interval $[a, b] .$ Then the arc length of the portion of the graph of $f (x)$ from the point $(a, f (a))$ to the point $(b, f (b))$ is given by

Arc Length = \int_{a}^{b} \sqrt{1 + {[f^{'} (x)]}^{2}} d x .

Note that we are integrating an expression involving $f^{'} (x),$ so we need to be sure $f^{'} (x)$ is integrable. This is why we require $f (x)$ to be smooth. The following example shows how to apply the theorem.

Calculating the arc length of a function of x

Let $f (x) = 2 x^{3 / 2} .$ Calculate the arc length of the graph of $f (x)$ over the interval $[0, 1] .$ Round the answer to three decimal places.

We have $f^{'} (x) = 3 x^{1 / 2},$ so ${[f^{'} (x)]}^{2} = 9 x .$ Then, the arc length is

\begin{matrix} Arc Length & = \int_{a}^{b} \sqrt{1 + {[f^{'} (x)]}^{2}} d x \\ = \int_{0}^{1} \sqrt{1 + 9 x} d x . \end{matrix}

Substitute $u = 1 + 9 x .$ Then, $d u = 9 d x .$ When $x = 0,$ then $u = 1,$ and when $x = 1,$ then $u = 10 .$ Thus,

\begin{matrix} Arc Length & = \int_{0}^{1} \sqrt{1 + 9 x} d x \\ = \frac{1}{9} \int_{0}^{1} \sqrt{1 + 9 x} 9 d x = \frac{1}{9} \int_{1}^{10} \sqrt{u} d u \\ = {\frac{1}{9} \cdot \frac{2}{3} u^{3 / 2} |}_{1}^{10} = \frac{2}{27} [10 \sqrt{10} - 1] \approx 2.268 units . \end{matrix}

Got questions? Get instant answers now!

Let $f (x) = (4 / 3) x^{3 / 2} .$ Calculate the arc length of the graph of $f (x)$ over the interval $[0, 1] .$ Round the answer to three decimal places.

$\frac{1}{6} (5 \sqrt{5} - 1) \approx 1.697$

Got questions? Get instant answers now!

Although it is nice to have a formula for calculating arc length, this particular theorem can generate expressions that are difficult to integrate. We study some techniques for integration in Introduction to Techniques of Integration . In some cases, we may have to use a computer or calculator to approximate the value of the integral.

Using a computer or calculator to determine the arc length of a function of x

Let $f (x) = x^{2} .$ Calculate the arc length of the graph of $f (x)$ over the interval $[1, 3] .$

We have $f^{'} (x) = 2 x,$ so ${[f^{'} (x)]}^{2} = 4 x^{2} .$ Then the arc length is given by

Arc Length = \int_{a}^{b} \sqrt{1 + {[f^{'} (x)]}^{2}} d x = \int_{1}^{3} \sqrt{1 + 4 x^{2}} d x .

Using a computer to approximate the value of this integral, we get

\int_{1}^{3} \sqrt{1 + 4 x^{2}} d x \approx 8.26815 .

Got questions? Get instant answers now!

Let $f (x) = sin x .$ Calculate the arc length of the graph of $f (x)$ over the interval $[0, π] .$ Use a computer or calculator to approximate the value of the integral.

$Arc Length \approx 3.8202$

Got questions? Get instant answers now!

Arc length of the curve x = g ( y )

We have just seen how to approximate the length of a curve with line segments. If we want to find the arc length of the graph of a function of $y,$ we can repeat the same process, except we partition the $y -axis$ instead of the $x -axis .$ [link] shows a representative line segment.

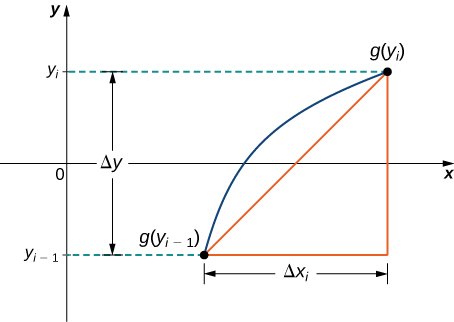
This figure is a graph. It is a curve to the right of the y-axis beginning at the point g(ysubi-1). The curve ends in the first quadrant at the point g(ysubi). Between the two points on the curve is a line segment. A right triangle is formed with this line segment as the hypotenuse, a horizontal segment with length delta x, and a vertical line segment with length delta y. — A representative line segment over the interval $[y_{i - 1}, y_{i}] .$

Then the length of the line segment is $\sqrt{{(Δ y)}^{2} + {(Δ x_{i})}^{2}},$ which can also be written as $Δ y \sqrt{1 + {((Δ x_{i}) / (Δ y))}^{2}} .$ If we now follow the same development we did earlier, we get a formula for arc length of a function $x = g (y) .$

Arc length for x = g ( y )

Let $g (y)$ be a smooth function over an interval $[c, d] .$ Then, the arc length of the graph of $g (y)$ from the point $(c, g (c))$ to the point $(d, g (d))$ is given by

Arc Length = \int_{c}^{d} \sqrt{1 + {[g^{'} (y)]}^{2}} d y .

Calculating the arc length of a function of y

Let $g (y) = 3 y^{3} .$ Calculate the arc length of the graph of $g (y)$ over the interval $[1, 2] .$

We have $g^{'} (y) = 9 y^{2},$ so ${[g^{'} (y)]}^{2} = 81 y^{4} .$ Then the arc length is

Arc Length = \int_{c}^{d} \sqrt{1 + {[g^{'} (y)]}^{2}} d y = \int_{1}^{2} \sqrt{1 + 81 y^{4}} d y .

Using a computer to approximate the value of this integral, we obtain

\int_{1}^{2} \sqrt{1 + 81 y^{4}} d y \approx 21.0277 .

Got questions? Get instant answers now!

Let $g (y) = 1 / y .$ Calculate the arc length of the graph of $g (y)$ over the interval $[1, 4] .$ Use a computer or calculator to approximate the value of the integral.

$Arc Length = 3.15018$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 2. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11965/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?

Ask

©flickr: Justin	Music Appreciation Final Practice By Madison Christian Start Exam
©flickr:	Arctic Ease Telemarketing Campaign Quiz By Nicole Duquette Start Quiz
	7 Biology 07 Cellular Respiration MCQ By OpenStax Start Quiz
	Computer Skills Literacy MCQ By LaToya Trowers Start Quiz
	22 AP Key Terms 22 The Respiratory System By OpenStax Start Key Terms
	Cultural Anthropology Assignment 2 By Richley Crapo Start Assignment
	Microeconomics Test 1 By IES Portal Start Test
	2 Human A&P 2- Test 2 By Madison Christian Start Flashcards
	Real Estate Finance Exam 2003 By Tod McGrath Start Exam
	Principles of Marketing By Dionne Mahaffey Start Quiz