| << Chapter < Page | Chapter >> Page > |
3.3 If you only receive the information as in the sketches below, can you say with certainty that the two triangles are a lw a ys congruent?

DEFρCBAρ3.4 Will the following two triangles be congruent? Why?
4.1 Study page A-4 of the accurately constructed triangles. All the triangles on page A-4 were constructed by using two sides and the angle not between the two given sides, (ss ) Study these triangles and write down the pairs of triangles which are congruent. Again remember to write down the triangles in order of the elements which are equal.
4.2 There are two triangles, which, although the two sides and the angle are equal, are not congruent. Name them.
4.3.1 Do you think that, if two sides and the angle not between the two sides, are used to construct triangles they would always be congruent?
4.3.2 What condition must the given sides satisfy for the triangles to be congruent?
4.4.4 If you only receive the information as in the sketches below, can you with certainty say that the two triangles are always congruent? (Remember you now do not know what the lengths of the two given sides).

4.5.1 There are four triangles on page A-4 where the given angle is 90°. If the angle not between the two given sides is equal to 90°, do you think that the two triangles will always be congruent? (rhs)
4.5.2 If you only receive the information like in the two sketches below, can you with certainty say that the two triangles are always be congruent?

5. On page A-5 there are triangles of which the three angles of the one triangle are equal to the three angles of the other triangle. ( )
5.1 Are the triangles constructed like this always necessarily congruent?
5.2 If you only receive the information like in the two sketches below, can you with certainty say that the two triangles are always be congruent?
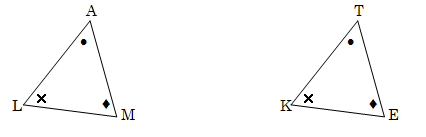
6. Now give the combinations of sides and angles for triangles to be congruent. Illustrate each combination as in the e x ample below:
1.

Homework assignment
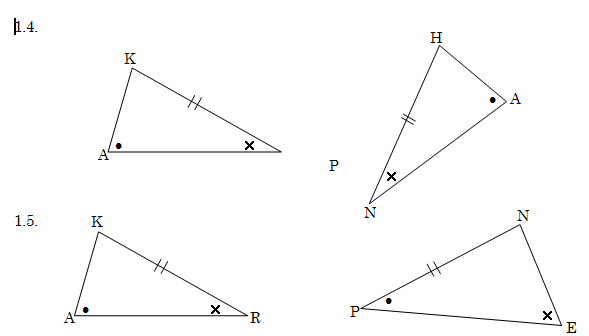
1. State whether the following pairs of triangles are congruent or not. Do each number like the example below.
Example:

A = D; B = E and C = F
N.B. If the triangles are not necessarily congruent, only write ΔABC ΔDEF and then write down why you say so.


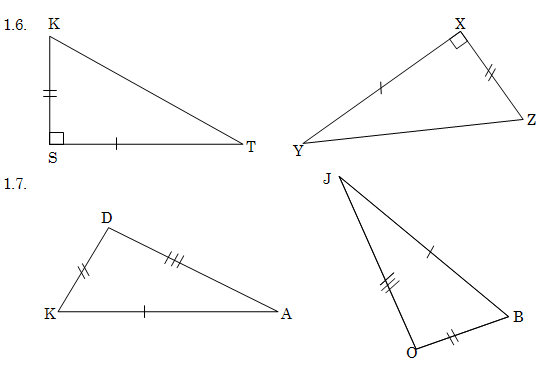

2. In each of the following pairs of triangles two pairs of equal elements are marked. In each case write down another pair of equal elements for the triangles to be congruent. Give the congruency test which you used and also give all the possibilities without repeating a congruency test.




| LO 3 |
| Space and Shape (Geometry)The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three-dimensional objects in a variety of orientations and positions. |
| We know this when the learner : |
| 3.1 recognises, visualises and names geometric figures and solids in natural and cultural forms and geometric settings, including:3.1.1 regular and irregular polygons and polyhedra;3.1.2 spheres;3.1.3 cylinders;3.2 in contexts that include those that may be used to build awareness of social, cultural and environmental issues, describes the interrelationships of the properties of geometric figures and solids with justification, including:3.2.1 congruence and straight line geometry;3.3 uses geometry of straight lines and triangles to solve problems and to justify relationships in geometric figures;3.4 draws and/or constructs geometric figures and makes models of solids in order to investigate and compare their properties and model situations in the environment; |
| 3.5 uses transformations, congruence and similarity to investigate, describe and justify (alone and/or as a member of a group or team) properties of geometric figures and solids, including tests for similarity and congruence of triangles. |

Notification Switch
Would you like to follow the 'Mathematics grade 9' conversation and receive update notifications?