| << Chapter < Page | Chapter >> Page > |
Another way of looking at this is that we're simpling doing a parallel to serial operation. Let's get on to the actual implementation in LabVIEW.
Block diagram layout
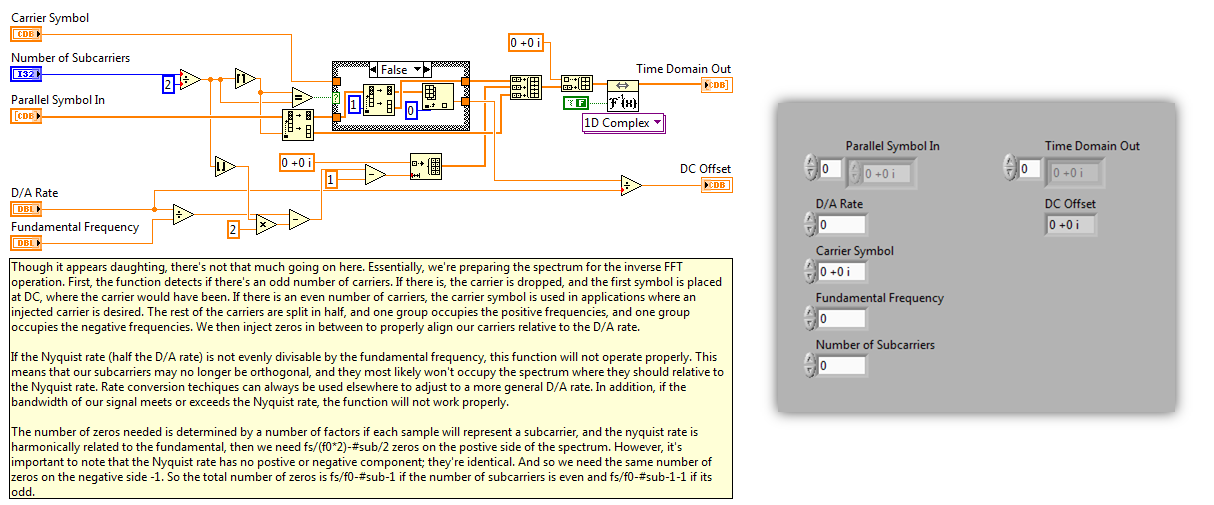
Above we see the actual block diagram. Though it can appear overwhelming, as long as the theory discussed above is understood, the rest is rather simple. In fact, everything we discussed above is nearly implemented in one block by the built in IFFT function! Everything we see surrounding it is put in place for user-friendliness and flexability.
In case an injected carrier for ease of receiving is desired, the user can specify a carrier symbol. The array size divided by two and rounding simply is to find out if there is an even or odd number of subcarriers. If even, the carrier specified is injected. If odd, the DC frequency is injected with the first symbol, so the lone symbol will take the place of the carrier for the sake of symettry. The reason the round toward infinity is used is simply because of the way the split array function works. The split array function simply truncates the number and cuts the array at that point, so by rounding up the odd carrier will always be in the first half.
The second half of the split is added to the end of the frequency domain. The only magic then appears in between: how many zeros do we inject and why? The answer isn't as direct, but it is a very fundamental concept. We want to conserve bandwidth, and so this is the motivation between bunching up the subcarriers as close to DC as possible. In addition, the easiest and most efficient way to make them orthogonal is to place a symbol at each sample. This way they're all related to the first non-DC frequency which is itself a fraction of the sampling (D/A) frequency.
Now, we want to ensure these relationships are maintained, as well as a few more. The user can specify the exact fundamental frequency desired, as well as the ultimate D/A rate. Two things must hold in the spectrum then: the fundamental frequency must be related to the D/A rate appropriately and in the first sample, and the Nyquist Rate of the system must be half the sampling frequency. If any of this is completely new, review the fundamentals of Digital Signal Processing (DSP). This constraint is the reason we choose the number of zeros, and why we want to choose our fundamental frequency such that sampling_freq/(2*fundamental_freq) is a whole number. Stated another way, the Nyquist Rate is evenly divisible by our fundamental. Once again, we can say the Nyquist Rate is an integer multiple of the Fundamental Frequency. This should be apparent from the above discussion. Afterall, halfway through our samples we should encounter the Nyquist Rate, the highest representable digital frequency, half the sampling rate. Every sample before this will be a fraction of this frequency. If this frequency exists at Sample 32, then our fundamental should be 1/32th of the Nyquist rate, as we will place it on a sample directly (no interpolation).
While a more generalized procedure is certainly possible, it's simply not practical in the face of transparency and computational complexity. In addition, sample rate conversion is a topic in and of itself, and any of those advanced techniques can be applied to the signal externally before transmission.
If you are still confused on how this works, check out the instructional and example video below or email the author for more questions. The sub-VI is available below for download.
Instructional video
Example video

Notification Switch
Would you like to follow the 'Fully configurable ofdm sdr transceiver in labview' conversation and receive update notifications?