| << Chapter < Page | Chapter >> Page > |
This set of notes presents the Support Vector Machine (SVM) learning algorithm. SVMs are among the best (and many believe are indeed the best) “off-the-shelf”supervised learning algorithm. To tell the SVM story, we'll need to first talk about margins and the idea of separating data with a large “gap.” Next, we'll talk about the optimal marginclassifier, which will lead us into a digression on Lagrange duality. We'll also see kernels, which give a way to apply SVMs efficiently in very highdimensional (such as infinite-dimensional) feature spaces, and finally, we'll close off the story with the SMO algorithm, which gives an efficient implementationof SVMs.
We'll start our story on SVMs by talking about margins. This section will give the intuitions about margins and about the “confidence” of our predictions; these ideaswill be made formal in "Functional and geometric margins" .
Consider logistic regression, where the probability is modeled by . We would then predict “1” on an input if and only if , or equivalently, if and only if . Consider a positive training example ( ). The larger is, the larger also is , and thus also the higher our degree of “confidence” that the label is 1. Thus, informally we can think of ourprediction as being a very confident one that if . Similarly, we think of logistic regression as making a very confident prediction of , if . Given a training set, again informally it seems that we'd have found a good fit to thetraining data if we can find so that whenever , and whenever , since this would reflect a very confident (and correct) set of classifications for all the training examples. This seems to be a nice goal toaim for, and we'll soon formalize this idea using the notion of functional margins.
For a different type of intuition, consider the following figure, in which x's represent positive training examples, o's denote negative training examples,a decision boundary (this is the line given by the equation , and is also called the separating hyperplane ) is also shown, and three points have also been labeled A, B and C.
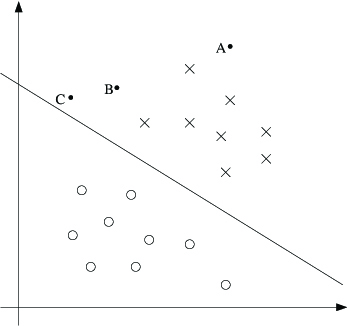
Notice that the point A is very far from the decision boundary. If we are asked to make a predictionfor the value of at A, it seems we should be quite confident that there. Conversely, the point C is very close to the decision boundary, and while it's on theside of the decision boundary on which we would predict , it seems likely that just a small change to the decision boundary could easily have caused our prediction to be . Hence, we're much more confident about our prediction at A than at C. The point B liesin-between these two cases, and more broadly, we see that if a point is far from the separating hyperplane, then we may be significantly more confident in our predictions.Again, informally we think it'd be nice if, given a training set, we manage to find a decision boundary that allows us to make all correct and confident (meaning far from thedecision boundary) predictions on the training examples. We'll formalize this later using the notion of geometric margins.

Notification Switch
Would you like to follow the 'Machine learning' conversation and receive update notifications?