2.1 Exponent concepts -- laws of exponents

The following are generally referred to as the “laws” or “rules” of exponents.

As with any formula, the most important thing is to be able to use them—that is, to understand what they mean. But it is also important to know where these formulae come from . And finally, in this case, the three should be memorized.

So...what do they mean? They are, of course, algebraic generalizations—statements that are true for any $x$ , $a$ , and $b$ values. For instance, the first rule tells us that:

which you can confirm on your calculator. Similarly, the third rule promises us that

These rules can be used to combine and simplify expressions.

Why do these rules work? It’s very easy to see, based on what an exponent is.

You see what happened? ${\text{19}}^3$ means three 19s multiplied; ${\text{19}}^4$ means four 19s multiplied. Multiply them together, and you get seven 19s multiplied.

Why does the second rule work?
First form	Second form
$\frac{{\text{19}}^8}{{\text{19}}^5}$	$\frac{{\text{19}}^5}{{\text{19}}^8}$
$=\frac{\text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}}{\text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}}$	$=\frac{\text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}}{\text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}\cdot \text{19}}$
$={\text{19}}^3$	$=\frac{1}{{\text{19}}^3}$

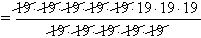In this case, the key is fraction cancellations . When the top is multiplied by 19 and the bottom is multiplied by 19, canceling these 19s has the effect of dividing the top and bottom by 19. When you divide the top and bottom of a fraction by the same number, the fraction is unchanged.

You can also think of this rule as the inevitable consequence of the first rule. If ${\text{19}}^3\cdot {\text{19}}^5={\text{19}}^8$ , then $\frac{{\text{19}}^8}{{\text{19}}^5}$ (which asks the question “ ${\text{19}}^5$ times what equals ${\text{19}}^8$ ?”) must be ${\text{19}}^3$ .

What does it mean to raise something to the fourth power? It means to multiply it by itself, four times. In this case, what we are multiplying by itself four times is ${\text{19}}^3$ , or $\left(\text{19}\cdot \text{19}\cdot \text{19}\right)$ . Three 19s multiplied four times makes twelve 19s multiplied.