| << Chapter < Page | Chapter >> Page > |
Resistances range over many orders of magnitude. Some ceramic insulators, such as those used to support power lines, have resistances of or more. A dry person may have a hand-to-foot resistance of , whereas the resistance of the human heart is about . A meter-long piece of large-diameter copper wire may have a resistance of , and superconductors have no resistance at all (they are non-ohmic). Resistance is related to the shape of an object and the material of which it is composed, as will be seen in Resistance and Resistivity .
Additional insight is gained by solving for yielding
This expression for can be interpreted as the voltage drop across a resistor produced by the flow of current . The phrase drop is often used for this voltage. For instance, the headlight in [link] has an drop of 12.0 V. If voltage is measured at various points in a circuit, it will be seen to increase at the voltage source and decrease at the resistor. Voltage is similar to fluid pressure. The voltage source is like a pump, creating a pressure difference, causing current—the flow of charge. The resistor is like a pipe that reduces pressure and limits flow because of its resistance. Conservation of energy has important consequences here. The voltage source supplies energy (causing an electric field and a current), and the resistor converts it to another form (such as thermal energy). In a simple circuit (one with a single simple resistor), the voltage supplied by the source equals the voltage drop across the resistor, since , and the same flows through each. Thus the energy supplied by the voltage source and the energy converted by the resistor are equal. (See [link] .)
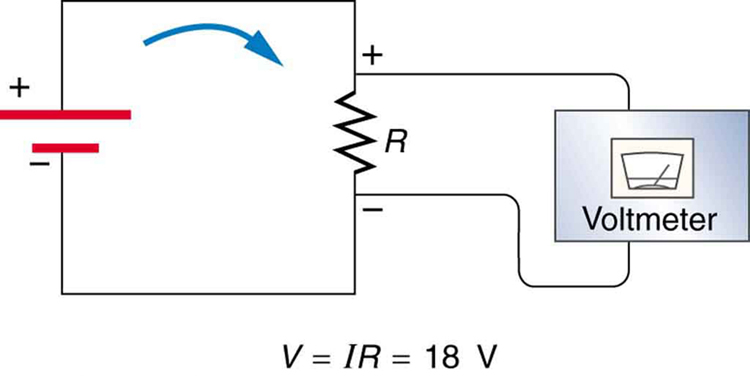
In a simple electrical circuit, the sole resistor converts energy supplied by the source into another form. Conservation of energy is evidenced here by the fact that all of the energy supplied by the source is converted to another form by the resistor alone. We will find that conservation of energy has other important applications in circuits and is a powerful tool in circuit analysis.
See how the equation form of Ohm's law relates to a simple circuit. Adjust the voltage and resistance, and see the current change according to Ohm's law. The sizes of the symbols in the equation change to match the circuit diagram.

The drop across a resistor means that there is a change in potential or voltage across the resistor. Is there any change in current as it passes through a resistor? Explain.
How is the drop in a resistor similar to the pressure drop in a fluid flowing through a pipe?
What current flows through the bulb of a 3.00-V flashlight when its hot resistance is ?
0.833 A
Calculate the effective resistance of a pocket calculator that has a 1.35-V battery and through which 0.200 mA flows.
What is the effective resistance of a car’s starter motor when 150 A flows through it as the car battery applies 11.0 V to the motor?
How many volts are supplied to operate an indicator light on a DVD player that has a resistance of , given that 25.0 mA passes through it?
(a) Find the voltage drop in an extension cord having a resistance and through which 5.00 A is flowing. (b) A cheaper cord utilizes thinner wire and has a resistance of . What is the voltage drop in it when 5.00 A flows? (c) Why is the voltage to whatever appliance is being used reduced by this amount? What is the effect on the appliance?
(a) 0.300 V
(b) 1.50 V
(c) The voltage supplied to whatever appliance is being used is reduced because the total voltage drop from the wall to the final output of the appliance is fixed. Thus, if the voltage drop across the extension cord is large, the voltage drop across the appliance is significantly decreased, so the power output by the appliance can be significantly decreased, reducing the ability of the appliance to work properly.
A power transmission line is hung from metal towers with glass insulators having a resistance of What current flows through the insulator if the voltage is 200 kV? (Some high-voltage lines are DC.)

Notification Switch
Would you like to follow the 'Physics 101' conversation and receive update notifications?