| << Chapter < Page | Chapter >> Page > |
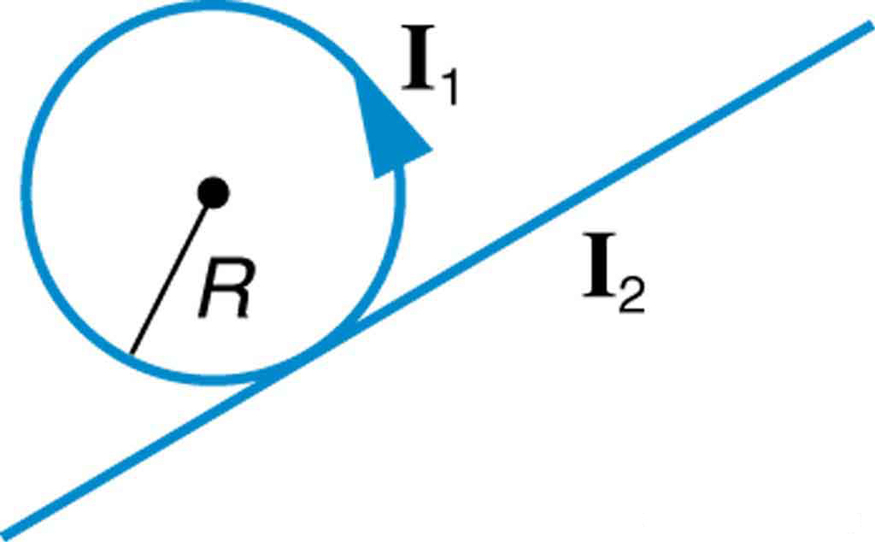
[link] shows a long straight wire just touching a loop carrying a current . Both lie in the same plane. (a) What direction must the current in the straight wire have to create a field at the center of the loop in the direction opposite to that created by the loop? (b) What is the ratio of that gives zero field strength at the center of the loop? (c) What is the direction of the field directly above the loop under this circumstance?
Find the magnitude and direction of the magnetic field at the point equidistant from the wires in [link] (a), using the rules of vector addition to sum the contributions from each wire.
,
Find the magnitude and direction of the magnetic field at the point equidistant from the wires in [link] (b), using the rules of vector addition to sum the contributions from each wire.
What current is needed in the top wire in [link] (a) to produce a field of zero at the point equidistant from the wires, if the currents in the bottom two wires are both 10.0 A into the page?
10.0 A
Calculate the size of the magnetic field 20 m below a high voltage power line. The line carries 450 MW at a voltage of 300,000 V.
Integrated Concepts
(a) A pendulum is set up so that its bob (a thin copper disk) swings between the poles of a permanent magnet as shown in [link] . What is the magnitude and direction of the magnetic force on the bob at the lowest point in its path, if it has a positive charge and is released from a height of 30.0 cm above its lowest point? The magnetic field strength is 1.50 T. (b) What is the acceleration of the bob at the bottom of its swing if its mass is 30.0 grams and it is hung from a flexible string? Be certain to include a free-body diagram as part of your analysis.
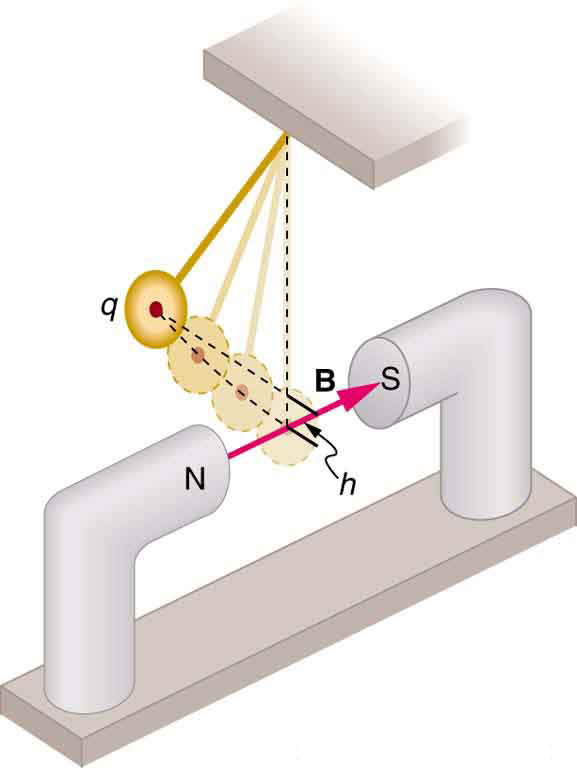
(a) upward
(b)
Integrated Concepts
(a) What voltage will accelerate electrons to a speed of ? (b) Find the radius of curvature of the path of a proton accelerated through this potential in a 0.500-T field and compare this with the radius of curvature of an electron accelerated through the same potential.
Integrated Concepts
Find the radius of curvature of the path of a 25.0-MeV proton moving perpendicularly to the 1.20-T field of a cyclotron.
60.2 cm
Integrated Concepts
To construct a nonmechanical water meter, a 0.500-T magnetic field is placed across the supply water pipe to a home and the Hall voltage is recorded. (a) Find the flow rate in liters per second through a 3.00-cm-diameter pipe if the Hall voltage is 60.0 mV. (b) What would the Hall voltage be for the same flow rate through a 10.0-cm-diameter pipe with the same field applied?
Integrated Concepts
(a) Using the values given for an MHD drive in [link] , and assuming the force is uniformly applied to the fluid, calculate the pressure created in (b) Is this a significant fraction of an atmosphere?
(a)
(b) Not a significant fraction of an atmosphere
Integrated Concepts
(a) Calculate the maximum torque on a 50-turn, 1.50 cm radius circular current loop carrying in a 0.500-T field. (b) If this coil is to be used in a galvanometer that reads full scale, what force constant spring must be used, if it is attached 1.00 cm from the axis of rotation and is stretched by the arc moved?

Notification Switch
Would you like to follow the 'Introductory physics - for kpu phys 1100 (2015 edition)' conversation and receive update notifications?