| << Chapter < Page | Chapter >> Page > |
Absolutely continuous examples
By use of the discrete approximation, we may get approximations to the sums of absolutely continuous random variables. The results on discrete variables indicatethat the more values the more quickly the conversion seems to occur. In our next example, we start with a random variable uniform on .
Suppose uniform . Then and .
tappr
Enter matrix [a b]of x-range endpoints [0 1]
Enter number of x approximation points 100Enter density as a function of t t<=1
Use row matrices X and PX as in the simple caseEX = 0.5;
VX = 1/12;[z,pz] = diidsum(X,PX,3);F = cumsum(pz);
FG = gaussian(3*EX,3*VX,z);length(z)
ans = 298a = 1:5:296; % Plot every fifth point
plot(z(a),F(a),z(a),FG(a),'o')% Plotting details (see
[link] )
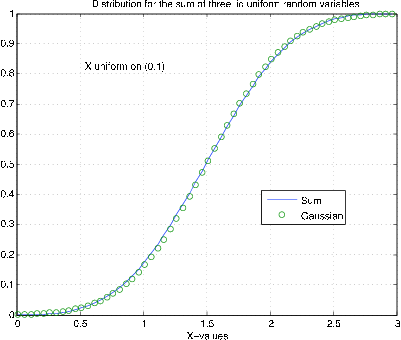
For the sum of only three random variables, the fit is remarkably good. This is not entirely surprising, since the sum of two gives a symmetric triangulardistribution on . Other distributions may take many more terms to get a good fit. Consider the following example.
Suppose the density is one on the intervals and . Although the density is symmetric, it has two separate regions of probability. From symmetry, . Calculations show . The MATLAB computations are:
tappr
Enter matrix [a b]of x-range endpoints [-1 1]
Enter number of x approximation points 200Enter density as a function of t (t<=-0.5)|(t>=0.5)
Use row matrices X and PX as in the simple case[z,pz] = diidsum(X,PX,8);VX = 7/12;
F = cumsum(pz);FG = gaussian(0,8*VX,z);
plot(z,F,z,FG)% Plottting details (see
[link] )
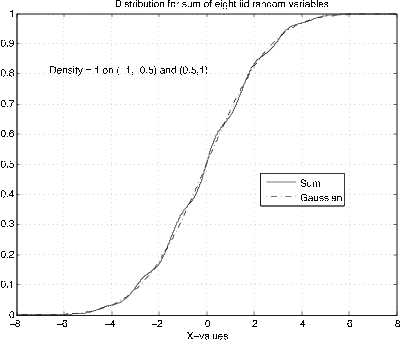
Although the sum of eight random variables is used, the fit to the gaussian is not as good as that for the sum of three in Example 4 . In either case, the convergence is remarkable fast—only a few terms are needed for good approximation.
The central limit theorem exhibits one of several kinds of convergence important in probability theory, namely convergence in distribution (sometimes called weak convergence). The increasing concentration of values of the sample average random variable A n with increasing n illustrates convergence in probability . The convergence of the sample average is a form of the so-called weak law of large numbers . For large enough n the probability that A n lies within a given distance of the population mean can be made as near one as desired. The fact that the variance of A n becomes small for large n illustrates convergence in the mean (of order 2).
In the calculus, we deal with sequences of numbers. If is a sequence of real numbers, we say the sequence converges iff for N sufficiently large a n approximates arbitrarily closely some number L for all . This unique number L is called the limit of the sequence. Convergent sequences are characterized by the fact that for largeenough N , the distance between any two terms is arbitrarily small for all . Such a sequence is said to be fundamental (or Cauchy ). To be precise, if we let be the error of approximation, then the sequence is

Notification Switch
Would you like to follow the 'Applied probability' conversation and receive update notifications?